Spectral Methods for Uncertainty Propagation and Quantification
Contents |
Object
As numerical models are becoming more and more efficient, the need for propagation and quantification of data uncertainty in simulation is growing. Specifically, we are interested in the characterization of the impact of uncertain model parameters in simulation outputs, such as boundary/initial conditions, physical properties of the medium, external forcing,... We are focusing on spectral methods for that purpose, which consist in the parametrization of uncertain inputs using a finite set of independent random variables. Then, the dependence of the simulation output with regards to the random variables is sought through a projection of the model solution on orthogonal (uncorrelated) basis functions. The projection coefficients are computed by means of Galerkin procedures, yielding a spectral method.
Methodological developments
A necessary condition for deriving efficient spectral techniques for uncertainty quantification (UQ) is the selection of a spectral basis suited to the solution dependence with regards to the random variables. Classically, one relies on basis functions made of continuous polynomials in the random variables (the so-called Polynomial Chaos expansions) which limits the applications to problems with smooth dependences. We have developed in [1,2] piecewise continuous approximations and multi-resolution schemes to extend spectral UQ to non-smooth problems. It involves the construction of an orthogonal multi-wavelets system.
One characteristic feature of spectral UQ is the independence of the solution for different realizations of the random variables. Therefore, the spectral expansion can be made local over smooth sub-regions of the random space. This fact has been exploited to derive partition domain approaches where local piecewise continuous solutions are sought over non-overlapping sub-domains, thus decreasing the size of the computational problem to be solved [3]. Moreover, local solutions being independent, the resolution can be fully parallelized.
However, strategies based on decomposition of the random domain rise the issue of constructing optimal partition of the parameter space. The objective is to optimize the trade-off between approximation error and computational cost. We have derived heuristic criteria for that purpose, which aims at refining the partition only where needed. We have also initiated a research program on the extension of deterministic a posteriori error analysis to the stochastic UQ problem [4].
Results and recent progresses
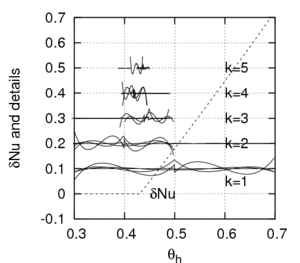
Figures 1 (a-c) shows the predicted heat-transfer enhancement coefficient
for a cavity filled with air and subjected to a random temperature
boundary conditions 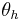 that can trigger the Rayleigh-Bénard instability
(critical temperature is
that can trigger the Rayleigh-Bénard instability
(critical temperature is 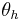 =0.43).
One can notice the details brought by the multi-wavelets at different resolution levels (
=0.43).
One can notice the details brought by the multi-wavelets at different resolution levels (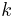 )
using the multi-resolution-analysis with polynomial order 1 to 3 (from a to c).
)
using the multi-resolution-analysis with polynomial order 1 to 3 (from a to c).
Figure 2 shows on the left, the mesh of the spatial/stochastic domain resulting from a adaptation procedure, based on a posteriori error analysis, for the resolution of the Burgers equation with uncertain viscosity [4]. The effect of the adaptation on the computed probability density function of the model output is depicted in the right-part of Figure 2.
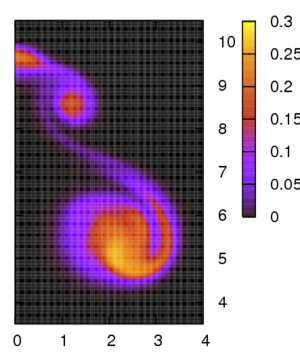
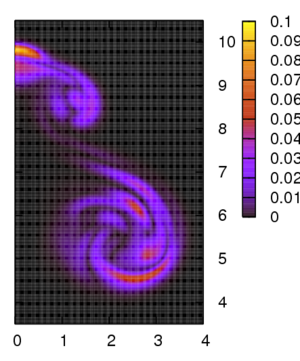
Figure 3 shows the mean (left) and variance (right) of the temperature field for a freely evolving hot patch of fluid in infinite domain, and uncertain characteristic Rayleigh number. The numerical method is based on a Lagrangian stochastic particle technique involving more than 200,000 computational elements [5].
References
[1] O. Le Maître, O. Knio, H. Najm and R. Ghanem, Uncertainty Propagation Using Wiener-Haar Expansions, J. Comput. Phys., 197(1), pp.28-57, (2004).
[2] O. Le Maître, H. Najm, R. Ghanem and O. Knio, Multi-Resolution Analysis of Wiener-Type Uncertainty Propagation Schemes, J. Comput. Phys., 197(2), pp.502-531, (2004).
[3] O. Le Maître, H. Najm, P. Pébay, R. Ghanem and O. Knio, Multi-Resolution Analysis for Uncertainty Quantification in Chemical Systems, J. Sci. Comput., 29, pp.864- (2007).
[4] L. Mathelin and O. Le Maître, Dual-Based a posteriori error estimate for stochastic finite element methods, Comm. App. Math. Comp. Sci., 2, pp.83-115,(2007).
[5] O. Le Maître and O. Knio, A stochastic particle-mesh scheme for uncertainty propagation in vortical flows, J. Comput. Phys., 226(1), pp.645-671, (2007).
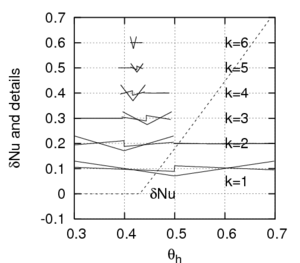
 as the function of the random temperature
as the function of the random temperature 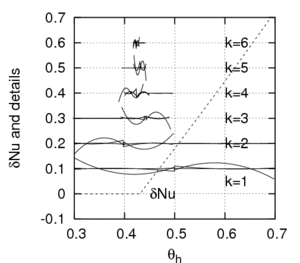
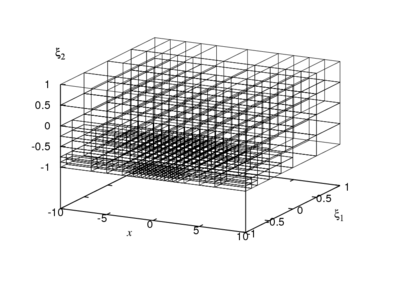
 ) and stochastic domain at the end of the refinement process, for the uncertain 1D Burgers equation (two random variables are used for the parametrisation of the fluid viscosity). The refinement is based on the a posteriori error estimation.
) and stochastic domain at the end of the refinement process, for the uncertain 1D Burgers equation (two random variables are used for the parametrisation of the fluid viscosity). The refinement is based on the a posteriori error estimation.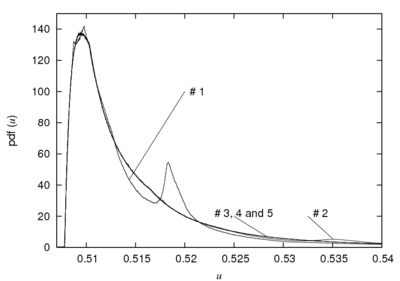
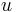 at a fixed spatial point
at a fixed spatial point