Approximation of PDE's in L1
J.L. Guermond in collaboration with B. Popov (Texas A&M Univ.)
Contents |
Object
I have been working on stabilization of noncoercive PDEs by means of two-level subgrid viscosity since 1997. In the continuity of this research I am currently developing a new theory for approximating PDEs
in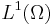 
by using finite elements. I collaborate on this program with Bojan Popov (Professor, "Texas A&M Univ.").
The method that we are proposing is a generalization of the Least-Squares method to non-Hilbertian settings. It is suitable for solving first-order PDEs in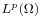 
, 
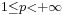. We have proved a priori and a posteriori error estimates for this formulation.
This research program is funded by "NSF DMS-0510650" (2005-2008).
Description
We have proved very innovative results:
- The best
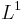-approximation converges to the viscosity solution of one-dimensional linear transport equations equipped with ill-posed boundary conditions.
- The best 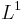-approximation for one-dimensional stationary Hamilton-Jacobi converges to the unique viscosity solution (under standard appropriate continuity and convexity assumptions on the Hamiltonian).
- The above convergence result for 1D stationary Hamilton-Jacobi equations is also true in two space dimensions on arbitrary triangulations and arbitrary polynomial approximations.
- We have constructed a fast algorithm for computing the best 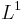-approximation of first-order PDEs in one space dimension. We have proved that the complexity is optimal (i.e. proportional to the number of unknown) for piecewise linear approximation and stationary Hamilton-Jacobi equations.
We are currently working on the two-dimensional generalization of our fast algorithm.
Results and prospect
Our numerical tests show (confirm) that the 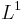-based technique approximates discontinuous solutions of PDEs without resorting to any artificial stabilization nor nonlinear slope limiters. This technique also computes viscosity (entropy) solutions of nonlinear PDE's. The price to be paid for this remarkable property is to solve a minimization problem with a functional which is not twice differentiable (i.e. the Newton method cannot be applied). Since the minimization problem can also be reformulated as a linear program, a possible alternative consists of using sophisticated linear programming algorithms.
We have not yet fully investigated this venue.
To finish, let us mention that our work seems to have non trivial connections with the so-called "compressed sensing" methods recently popularized by Candès/Donoho/De Vore/Tao. In particular, our minimization technique has similar "sparsity" properties. More precisely, the 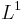functional
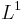to be minimized is the sum of the absolute value of residuals (the residuals are the PDE evaluated at the Gauss points of the triangulation). In general there are more residuals than unknowns. A striking characteristics of the -minimization is that the minimizers maximizes the number of residual
that are zero. In other words, the residual vector of the 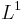-minimizer is the sparsest possible. By comparisons, the best 
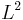-approximation is such that no residual is zero in general, i.e. the residual vector is full. One way to reformulate this property is that the best 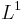-minimizer actually solved the PDEs at a number of Gauss points equal to the number of unknown whereas the 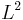-approximation does not solve the PDEs at any Gauss points.
References
See Publications