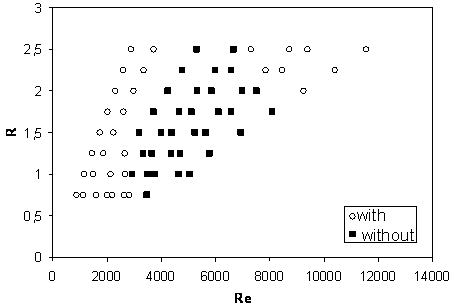Characterization of the flow topology past an open cavity and reduction of the dynamics complexity

From 2007 Scientific Report

Jump to: navigation, search

F. Lusseyran, Th. Faure, L. Pastur, Y. Fraigneau and B. Podvin

1 Object
2 Description
3 Results
- 3.1 Parametric investigation of the flow morphology
- 3.2 Dynamical reduction and topological characterization
4 Perspectives
5 References
6 Links

Object

Flow over open cavities is a test case for several problems of industrial interest. The cavity can indeed mimic structural discontinuities, such as car open roofs, landing gear cavities in airplanes, or cavities on the top of high speed trains, but also at lower velocity can represent problems of matter and heat transfers in cavity-like systems. This research is conducted within the theme "Unsteady Flows" of the group [[AERO]Unsteady Aerodynamics]. It aims at describing the coupling between the flow structures for a medium range Reynolds number Re between 860 and 32300) subsonic flow, with the purpose of implementing control techniques. One of the present challenging tasks, from a fundamental viewpoint as well as a practical one, lays in our ability to optimally control this kind of flow, so as to increase the aerodynamical performances, at the minimum cost. The experimental configuration investigated is the interaction between a laminar boundary layer and an open cavity, which aspect ratio R = L / H (length over height) is varied from 0.25 to 2.5.

Description

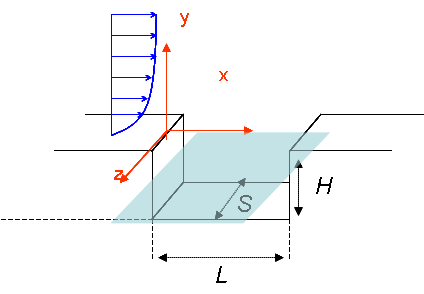
The study is performed in both an experimental setup (Figure 1), using LDV (laser Doppler velocimetry), PIV (particle image velocity) techniques and visualizations of the unsteady dynamic flow features in various planes of observation, and direct 3D numerical simulations based on the Navier-Stokes equations, in the incompressible domain. Our aim is to reduce the flow complexity by identifying some characteristic features of the flow, such as coherent stuctures, or by identifying underlying dynamical systems.

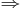
	$\Rightarrow$ $\Rightarrow$
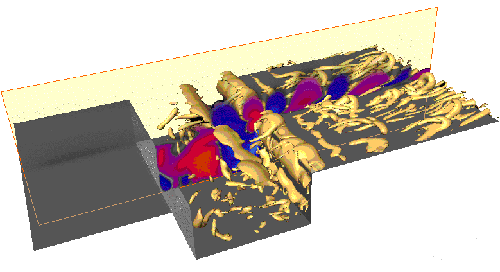
Figure 1. Cavity scheme and iso-factor Q of a DNS

Results

Parametric investigation of the flow morphology

Three-dimensional spanwise structures are developing in the flow generated by the interaction between a boundary layer and an open cavity. This 3D-segmentation is even stronger at middle external speed than at high speed corresponding the aero-acoustic interaction. The study of the cavity ﬂow with aspect ratio and Reynolds number has shown three morphological behaviors, explored through flow visualizations and measures of the velocity field.

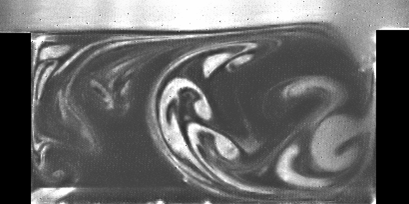
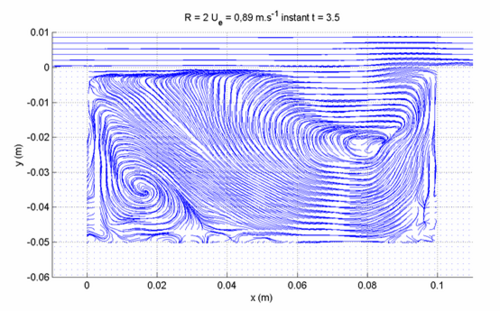
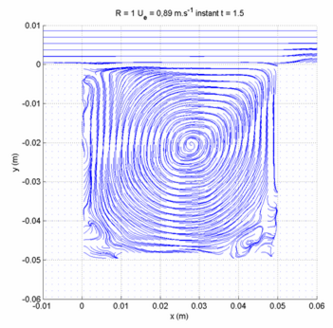
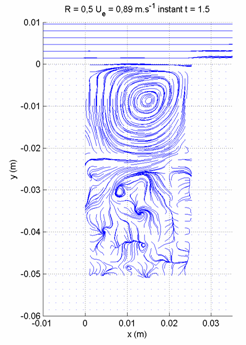
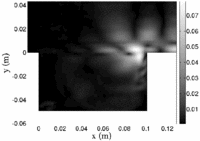
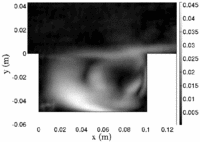
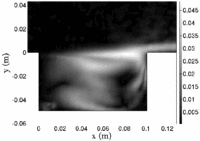
PIV measurements, using an optical flow technique with dynamical programming, have been therefore conducted for cavity aspect ratios from R = 0.5 to 2 and for Reynolds number between 1150 and 10670. They are conducted in a (x,y) plane in cavity midspan and confirmed results obtained by flow visualizations (Figure 2)[Faure et al. 2005 a,b]. The streamlines of an instantaneous field show the dynamical flow morphology with a high accuracy despite of a strong velocity gradient between the cavity flow and the external flow. For R = 2, the flow exhibits a main vortex in the downstream part of the cavity and a secondary counter-rotating vortex in the upstream part of the cavity (Figure 3). This secondary vortex is limited to a corner vortex for R = 1 (Figure 4). For R = 2 to 1, the main vortex spreads on the entire cavity height but is limited to the upper half of the cavity for R = 0.5 (Figure 5) [Faure et al. 2007, b].

Figure 2. Flow morphology visualized by smoke injection in a midspan (x,y) plane inside the cavity for R = 2.


Figure 3. Flow morphology and streamlines in a midspan (x,y) plane inside the cavity for R = 2.	Figure 4. Flow morphology and streamlines in a midspan (x,y) plane inside the cavity for R = 1.	Figure 5. Flow morphology and streamlines in a midspan (x,y) plane inside the cavity for R = 0.5.

In order to understand the spatial development of flow instabilities, visualizations are carried out in a (x,z) plane located inside the cavity. The issue is to emphasize the three-dimensional development of the flow. In particular, we show that the cavity dynamical structures are not due to secondary shear layer instabilities. The study is conducted by changing the cavity length and height and the external flow velocity, and therefore the existence or non-existence of the longitudinal instabilities is addressed. These instabilities are resulting of an imbalance between centrifugal forces and radial pressure gradient, where the centrifugal forces are caused by the motion of the main cavity vortex. The flow instabilities can be identified as pairs of counter-rotating vortices inside the cavity (Figure 6) and correspond to the Görler linear instability mecanisme (Figure 7). They are also isolated pairs of counter-rotating vortices that do not form a loop, identified as Görtler vortices (Figure 8).

Figure 6. Görtler diagram of stability from Swearingen 1987; the stars correspond to our measurements.

Figure 7. Development of annular Görtler-like instabilities inside the cavity for R = 1 and Re = 4233: view in a (x,z) plane.

Figure 8. Development of Görtler-like instabilities inside the cavity for R = 0.5 and Re = 7500: view in a (x,z) plane.

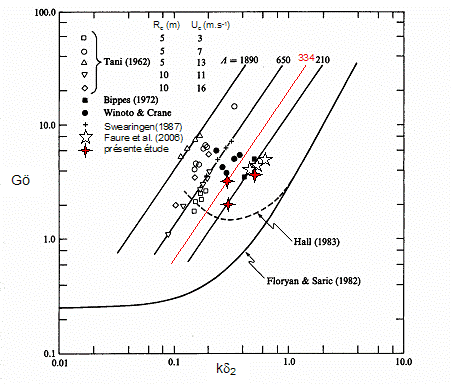
The investigation of the range R = 0.25 to 2.5 and Re = 860 to 14000 of flow visualizations shows the domain of existence of the instabilities, as functions of Reynolds number and aspect ratio (Figure 9). The region where instabilities vortices are present in the plane (R, Re) is forming a compact domain.

Figure 9. Existence diagram of the instabilities for different aspect ratio and Reynolds numbers.

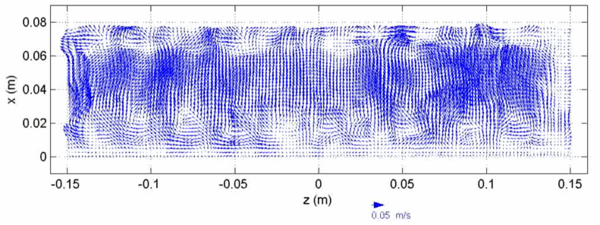
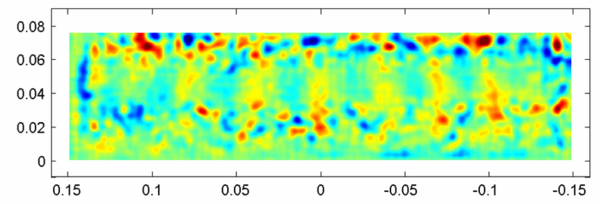
The instabilities are also confirmed from visualisation by PIV measurements (Figure 10). The presence of the pairs of counter-rotating vortices is identified by the y-component of the vorticity as blue and red regions along the cavity upstream and downstream walls (Figure 11) [Faure et al. 2007, a].


Figure 10. PIV mesurements of the velocity in a (x,z) plane for R = 1.5 and Re = 4450.	Figure 11. Component of the vorticity component orthogonal to the (x,z) plane for R = 1.5 and Re = 4450.

Dynamical reduction and topological characterization

Coherent structures have been extracted out of the flow by applying a proper orthogonal decomposition (POD). The decomposition is performed on either the fully 3D velocity fields computed by DNS, 2D restrictions of the numerical flow such as to mimic the experimental data available from 2D PIV snapshots, or directly to the experimental PIV snapshots (Figure 12). Although the convergence towards the "true" coherent structures is slower in the 2D case than in the 3D case, we have shown that the POD can achieve, at least in the longitudinal plane, a fairly good separation of the coherent structures initiated within the shear layer from the structures confined inside the cavity [Pastur et al. :Phys. Rev. E, 72, 065301(R) (2005)].


Figure 12. First four coherent structures identified by POD in 2D PIV snapshots.

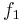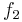From time-resolved LDV measurements, we have shown that, over a wide range of the Reynolds number, the shear layer is the theatre of a nonlinear competition between two modes of oscillation, whose frequencies $f_1$ and $f_2$ depend on 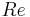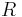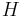$Re$ , $R$ , $H$ . In the experiment, both modes tend to exclude each other over time (Figure 12). Surprisingly, the DNS flow does not exhibit such a dual mode competition, although the running and limit conditions are analogous to the experimental ones. A breakthrough in the study of the coherent structures has been achieved by synchronizing (time-resolved) LDV mesurements to (space-resolved) PIV snapshots. Indeed, from the LDV well-resolved cycle of oscillation, it has become possible to sort the temporally sparsed PIV snapshots in phase with the shear layer oscillations [Faure et al. 2006].


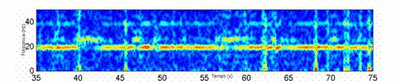
Figure 13. Axial velocity spectrogram downstream of the cavity for Ue = 1,75 m.s-1 and R = 2.

Phase averaging the velocity field snapshots at a given phase 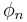$\phi _n$ of the cycle of oscillation, and varying 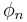$\phi _n$ , provides the spatial sequence of the mean cycle of oscillation shown in Figure 14. Each mean phase field 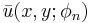$\bar{u}(x,y;\phi _n)$ still exhibits the unstable wave developping in the shear layer, while smoothing out the instantaneous velocity fluctuations. Therefore, it provides an efficient way for estimating the wavelength of the spatially growing unstable wave.

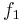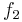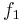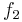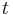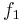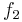In order to identify which coherent structures may be associated to each mode $f_1$ and $f_2$ , one must introduce criterions to decide whether mode $f_1$ or $f_2$ is present in the shear layer, at any given time $t$ . This is done using Hilbert-based complex demodulation of the LDV signal, around each mode $f_1$ and $f_2$ . 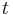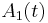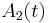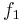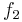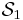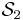Recovering at any time $t$ the instantaneous amplitudes $A_1(t)$ and $A_2(t)$ of the modes $f_1$ and $f_2$ , and comparing them to some threshold value (for example the mode mean amplitudes), it becomes possible to separate furthermore the PIV snapshots into two subsets $\mathcal{S}_1$ and $\mathcal{S}_2$ , each corresponding to a given mode of the shear layer instantaneous oscillation. 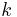The knowledge of the dispersion relation (not known yet), determined by plotting the LDV measured pulsation $\omega$ versus the mean phase field extracted wavenumber $k$ , would help in disciminating between the different models of the cavity flow dynamics.


Figure 14. Averaged cycle of the cavity flow obtained by phase averaging LDV-synchronized time-sparsed PIV snapshots.

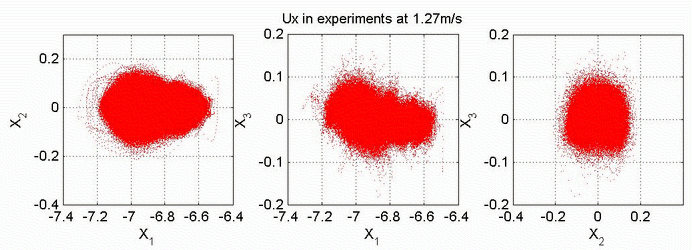
LDV measurements, spatially localized downstream of the cavity, exhibit dynamical behaviours whose fractal dimension remain less than 5 (Figure 15). This means that the flow underlying dynamics can reasonably be considered as strongly be deterministic.


Figure 15. 2D views of the 3D phase space portrait of the embedded LDV signal.

In the DNS flow, we have shown that the fully 3D space-time behaviour of the flow could be reconstructed from 2D restrictions of the 3D coherent structures determined by POD [Podvin et al], which open new perspectives for reconstructing fully 3D flows from simple 2D observations.

Perspectives

Two main aspects of the cavity flow will be under investigation in the next two years.

Using time-resolved (high speed) PIV, we plan to simultaneously determine the velocity and acceleration fields in the cavity flow. From their simultaneous knowledge, it may become possible to identify the dynamical system underlying the temporal dynamics of the coherent structures extracted by the POD. This work will be conducted in the framework of the HiSpeed ANR contract.
The flow topological squeleton does not keep very much degree of freedom to the flow, which has to conform to it. Henceforth, its knowledge would provide a very efficient tool for designing black boxes for flow control applications. This work will be supported by the DIB ANR contract, in collaboration with the LEA (Poitiers) and Peugeot.

References

PASTUR, L. R., LUSSEYRAN, F., FAURE, Th. M., FRAIGNEAU, Y., PETHIEU, R., DEBESSE, Ph. (2007) Quantifying the non-linear mode competition in the flow over an open cavity at medium Reynolds number, Experiments in Fluids (accepted)

FAURE, Th. M., ADRIANOS, P., LUSSEYRAN, F., PASTUR, L. R. (2007, b) Visualizations of the flow inside an open cavity at medium range Reynolds numbers, Experiments in Fluids, vol. 42, n°2, pp. 169-184

FAURE, Th. M., PECHLIVANIAN, N., LUSSEYRAN, F., PASTUR, L. R. (2007, a) Apparition de structures tourbillonnaires de type Görtler dans une cavité parallélépipédique ouverte de forme variable, Actes du 18ème Congrès Français de Mécanique, CFM2007-0008, Grenoble, 27-31 août 2007

LUSSEYRAN, F., PASTUR, L. R., FAURE, Th. M., PETHIEU, R. (2007) Structures tourbillonnaires cohérentes et intermittence des modes fréquentiels dans un écoulement en cavité ouverte, Actes du 18ème Congrès Français de Mécanique, CFM2007-1197, Grenoble, 27-31 août 2007

PETHIEU, R., PASTUR, L. R., LUSSEYRAN, F., DEBESSE, Ph., FAURE, Th. M. (2007) Caractérisation expérimentale de la compétition non-linéaire de modes de Kelvin-Helmholtz dans un écoulement en cavité, 10ème Rencontre du Non-Linéaire, Paris (France), 14-16 Mars 2007, pp. 143-148

FAURE, Th. M., LUSSEYRAN, F., PASTUR, L. R., PETHIEU, R., DEBESSE, Ph. (2006) Développement d’instabilités dans un écoulement subsonique se développant au-dessus d’une cavité : mesures synchronisées PIV-LDV, 10ème Congrès Francophone de Techniques Laser, Toulouse (France), 19-22 Septembre 2006, pp. 577-584

LUSSEYRAN, F., PASTUR, L. R., DEBESSE, Ph., FAURE, Th. M. (2005) Dynamique locale de l'écoulement dans une cavité ouverte, 5e Colloque de Chaos Temporel et de Chaos Spatio-temporel, Le Havre (France), 12-13 Décembre 2005, pp. 63-68

PASTUR, L. R.,LUSSEYRAN, F., FRAIGNEAU, Y., PODVIN, B. (2005) Determining the Spectral Signature of Spatial Coherent Structures, Physical Review E, Phys. Rev. E, 72, 065301(R).

PASTUR, L. R., LUSSEYRAN, F., FAURE, Th. M., FRAIGNEAU, Y., GOUGAT, P. (2005) Dynamical reduction of a subsonic flow over a cavity with an aim of control, 6th SIAM Conference on Control and its Applications, New Orleans (USA), July 11-14, 2005

LUSSEYRAN, F., FAURE, Th., ESCHENBRENNER, C. & FRAIGNEAU, Y.(2004) Shear layer instability and frequency modes inside an open cavity, 21st International Congress of Theoretical and Applied Mechanics, Warsaw (Poland), August 15-21, 2004, FM13S_10188.

FAURE, Th. M., DEBESSE, Ph., LUSSEYRAN, F., GOUGAT, P. (2005, b) Structures tourbillonnaires engendrées par l’interaction entre une couche limite laminaire et une cavité, 11ème Colloque de Visualisation et de Traitement d’Images en Mécanique des Fluides, Lyon (France), 6-9 Juin 2005 -

FAURE, Th. M., ADRIANOS, P., DEBESSE, Ph., LUSSEYRAN, F., PASTUR, L. R. (2005, a) Dynamique tourbillonnaire 3D dans une cavité ouverte de rapport de forme variable, 6ème Journée de Dynamique des Fluides sur le Plateau, Université Paris XI, Orsay, 14 Novembre 2005 -

Links

AERO