Coupling of natural convection with radiation in 2D square cavities
C. Perrotin, S. Xin (CETHIL), A. Sergent and P. Le Quéré, in collaboration with G. Grasseau (IDRIS)
Contents |
Objectives
This work is part of the COCORAPHA project the aim of which is to determine the most appropriate level of modelization to predict coupled convective and radiative heat transfer for the optimization of thermal efficiency of buildings. In this study we focus our attention on natural convection and radiative heat transfer in a 2D air-filled differentially heated square cavity which is a generic prototype configuration for these applications (see Fig. 0). To this aim, we want to develop a generic way to couple different programs each one specialised in one of the two heat transfer modes involved. In order to develop this coupling methodology we chose to couple a natural convection code written by Shihe Xin which solves the Navier-Stokes equations under the Boussinesq assumption with a numerical scheme based on the finite differences method. The radiation code is developed by Denis Lemonnier (Laboratoire d'Etudes Thermiques (LET) - Poitiers). It solves the radiative transfer equation by means of the discrete ordinates method (DOM). This code was improved to carry out simulations with a real-gas model using the spectral line weighted sum of grey gases (SLW) model. The coupling was implemented using CORBA with the grateful help of Gilles Grasseau (IDRIS: Institut du Développement et des Ressources en Informatique Scientifique - Orsay) in the DEISA (Distributed European Infrastructure for Supercomputing Applications) environment.
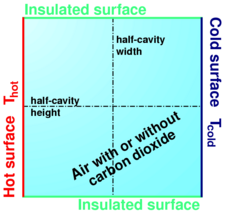
Apart from numerical set-up explicitly specified in the text, we use throughout this section a representation of the experimental cavity studied by Nicolas Rouger (LET - Poitiers).
This representation is composed by four one meter long walls with a thermal difference between isothermal walls set to 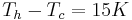 . The reference temperature is equal to
. The reference temperature is equal to 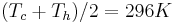 and the fluid parameters are such that this configuration leads to a Rayleigh number (
and the fluid parameters are such that this configuration leads to a Rayleigh number (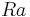 ) of
) of 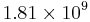 .
.
The four walls are assumed to be diffuse-grey surfaces with the same emissivity value (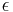 ) and radiative properties of the gaz mixture are assumed to be constant in the cavity.
) and radiative properties of the gaz mixture are assumed to be constant in the cavity.
In the following, we start by studying natural convection and gradually take into account radiation on surfaces and in the media.
Coupling of natural convection with surface radiation
For a given Rayleigh number, the flow configuration is defined by the cavity height (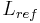 ) and the walls emissivity (
) and the walls emissivity (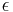 , see Fig. 3(a) & 3(b)).
Increasing
, see Fig. 3(a) & 3(b)).
Increasing 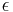 (see Fig. 1) or
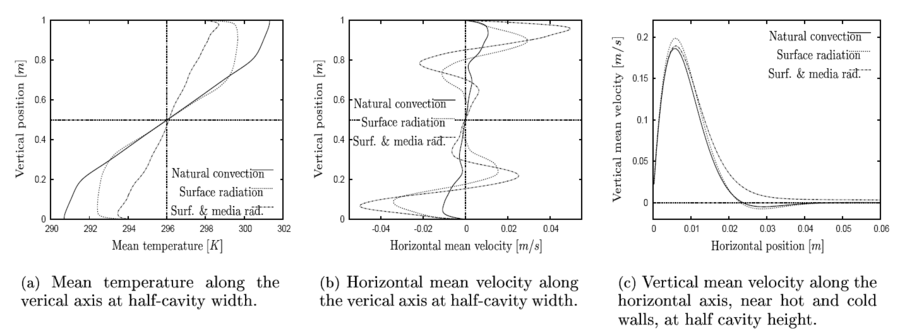
(see Fig. 1) or 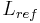 consequently reduces the thermal stratification in the cavity core (see Fig. 1(a)), increases the mean velocities in the boundary layers (see Fig. 1(b) & 1(c)) and increases the radiative heat flux on walls.
consequently reduces the thermal stratification in the cavity core (see Fig. 1(a)), increases the mean velocities in the boundary layers (see Fig. 1(b) & 1(c)) and increases the radiative heat flux on walls.
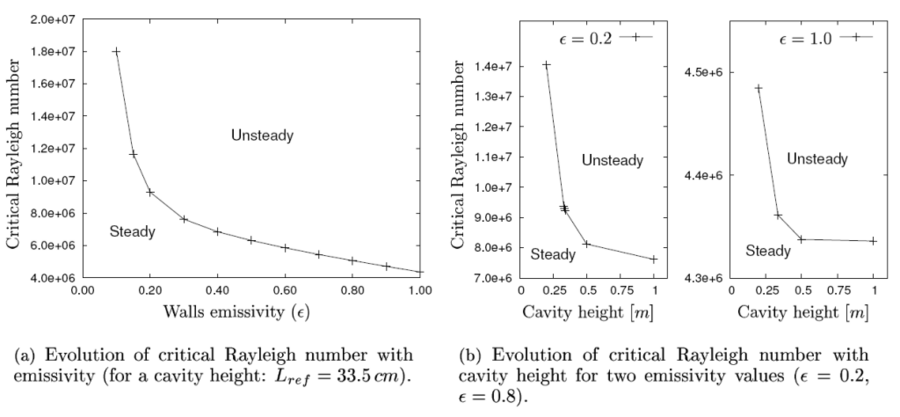
H. Wang et al [1] noticed that the transition to unsteadiness (corresponding to the critical Rayleigh number 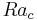 ) is trigged earlier by surface radiation when
) is trigged earlier by surface radiation when 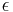 increases.
We performed additional computations for several emissivity values (see Fig. 2(a)) and observe a similar behavior when
increases.
We performed additional computations for several emissivity values (see Fig. 2(a)) and observe a similar behavior when 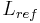 increases (see Fig. 2(b)).
increases (see Fig. 2(b)).
Influence of a participating medium corresponding to a grey-gas
In this paragraph we consider the gas to be a participating medium without scattering: it means that the radiative energy emitted by the fluid or a wall is partially absorbed in its direction of propagation by the fluid. The radiative properties of the fluid are modelled as a grey-gas (see Fig. 3(c)). Such a grey-gas is characterised by its absorption coefficient (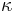 ); the particular case of a transparent medium corresponds to
); the particular case of a transparent medium corresponds to 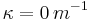 .
A participating medium is then defined by
.
A participating medium is then defined by 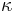 greater than zero.
Hence, an increase of
greater than zero.
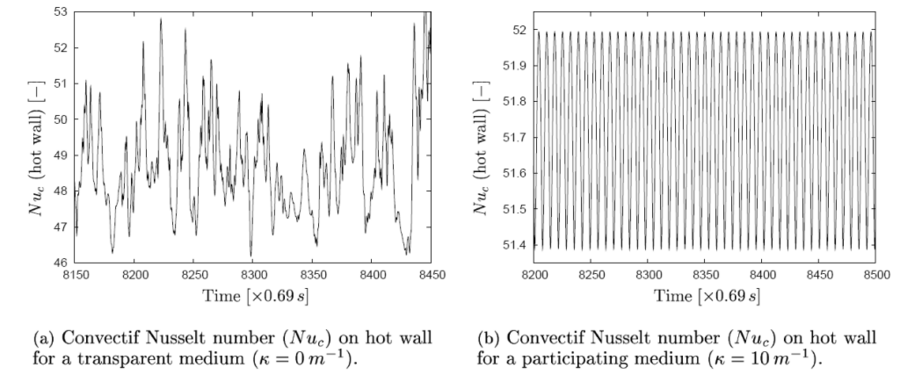
Hence, an increase of 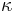 results in a stronger homogenisation of the temperature field (see Fig. 1(a)) and in a stabilization of the flow behavior (see Fig. 4): at
results in a stronger homogenisation of the temperature field (see Fig. 1(a)) and in a stabilization of the flow behavior (see Fig. 4): at 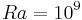 flow is chaotic in a transparent medium while it is periodical in a participating medium.
In both media, wall heat energy is transmitted to the fluid by both convection and radiation.
In a participating medium radiative heat transfer applies also to the fluid and it is especially
the case for fluid near the two vertical isothermal walls. This explains why
flow is chaotic in a transparent medium while it is periodical in a participating medium.
In both media, wall heat energy is transmitted to the fluid by both convection and radiation.
In a participating medium radiative heat transfer applies also to the fluid and it is especially
the case for fluid near the two vertical isothermal walls. This explains why 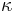 and the boundary layer thickness near isothermal walls increase jointly (see Fig 1(c)). In addition we notice that,
compared with the case of surface radiation, horizontal mean velocity increases further
near the horizontal adiabatic walls (see Fig. 1(b)) .
and the boundary layer thickness near isothermal walls increase jointly (see Fig 1(c)). In addition we notice that,
compared with the case of surface radiation, horizontal mean velocity increases further
near the horizontal adiabatic walls (see Fig. 1(b)) .
Simulations performed at moderate Rayleigh number lead to the same observations (see [2]).
Coupling of natural convection with radiation using a real-gas model
Because of the complexity of the radiative spectrum of a fluid, we cannot rigorously link the radiative properties of a gaz mixture to a single value of 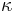 .
For a more realistic simulation we need to use a real-gas model such as the Spectral Line-based Weighted sum of grey-gases (SLW) model [3].
This method assimilates a real-gas as a sum of
.
For a more realistic simulation we need to use a real-gas model such as the Spectral Line-based Weighted sum of grey-gases (SLW) model [3].
This method assimilates a real-gas as a sum of 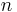 grey-gases, weighted by the mixture characteristics.
grey-gases, weighted by the mixture characteristics.
In spite of the care we took to carry out these 2D numerical simulations (See movie [1] ), detailed comparisons with experimental measurements are not satisfactory because the experimental configuration is fully 3D.
Future work
In order to have meaningful comparison between numerical and experimental results on the one hand and determine the most appropriate level of radiative heat transfer modelization, it will be necessary to perform 3D computations and couple 3D Navier-Stokes and radiative heat transfer codes.
Acknowledgments
We would like to thank Denis Lemonnier (Laboratoire d'Etude Thermique (LET) - Poitiers) for his fruitfuldiscussions and Nicolas Rouger (LET) for making available his experimental results. We are also grateful to Gilles Grasseau (Idris - Orsay) for the stimulating discussions and his help in implementing CORBA for code coupling.
References
[1] H. Wang, S. Xin, P. Le Quéré, Etude numérique du couplage de la convection naturelle avec le rayonnement de surfaces en cavité carrée remplie d'air, Comptes Rendus de Mécanique, 334, pp. 48-57 (2006).
[2] DEISA - Public Deliverables, Grid-enabling the second set of projects: status report of the first production releases. (May 16, 2006), http://www.deisa.org/files/DEISA-D-JRA6-4.pdf
[3] M. K. Denison, B. W. Webb, Development and application of an absorption-line blackbody distribution function for 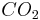 , Int. J. Heat Mass Transfer, 38, pp. 1813-1821 (1995).
, Int. J. Heat Mass Transfer, 38, pp. 1813-1821 (1995).
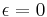 ,
, 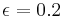 ,
, 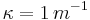 ).
).
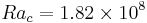 .
.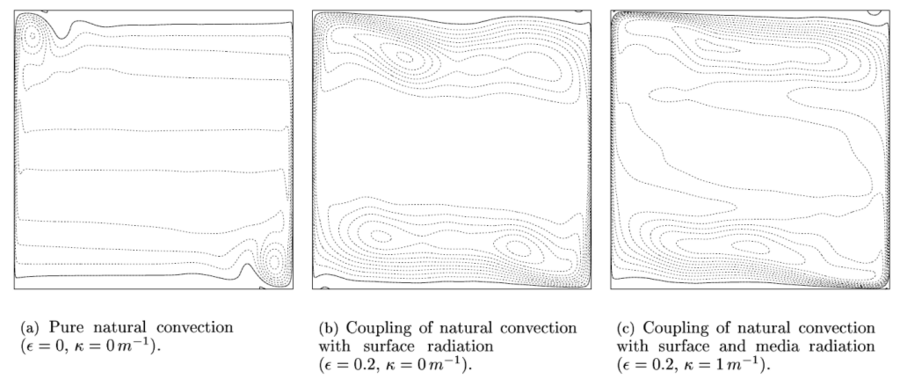
 ). Continuous lines represent
). Continuous lines represent  whereas dashed lines symbolize
whereas dashed lines symbolize  (with a increment
(with a increment 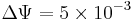 ).}
).}
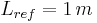 ,
, 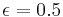 ,
, 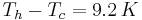 and
and