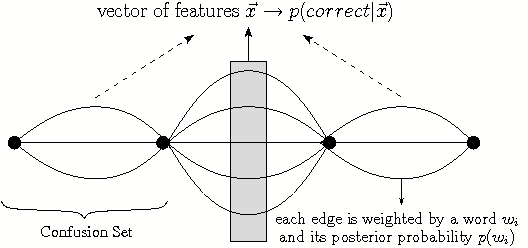
Error detection in confusion network
Contents |
Objective
In this work, error detection for broadcast news transcription is addressed in a post-processing stage. We investigate a logistic regression model based on features extracted from confusion networks. This model aims at estimating a confidence score for each confusion set as well as detecting errors. Different kinds of knowledge sources are explored and evaluated such as the confusion set alone, the statistical language model, and lexical properties.
Features for error detection
In this work, confusion networks are used as inputs for error detection. As defined in [4], a confusion network is a compact and linear graph, where the complexity of a word lattice is reduced to a serie of confusion sets. Each set represents time-parallel hypothesized words with their associated posterior probabilities. The words with the highest posterior in each confusion set are hypothesized. Compared to other ASR outputs, a confusion network :
- is a richer representation than one-best hypothesis and its posterior probability,
- does not contain the redundancy of a n-best list, and
- is more compact and efficient to handle than a word lattice.
As depicted in Figure 1, a vector of features 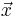 is obtained from each confusion set
(CS). The choice of the features are derived from [1],[2],[3],[5]. Three types of features are defined according to the involved
knowledge sources:
is obtained from each confusion set
(CS). The choice of the features are derived from [1],[2],[3],[5]. Three types of features are defined according to the involved
knowledge sources:
- The "CS" features are directly derived from the confusion set itself:
- best posterior probability and entropy of the posterior distribution
- duration and length, in number of characters, of the hypothesized word,
- length of the confusion network, and position of the set in the network
- two boolean features indicating whether the adjacent set has the null edge as the most probable word.
- Language model (LM) features rely on probabilities estimated with an n-gram LM on the confusion network: n-gram likelihood of the hypothesis; the best likelihood; the sum of the probabilities of all possible n-grams in the confusion network that can predict the hypothesized word.
- Lexical features depend on lexical information about the hypothesized word of the CS: the unigram probability, the lexical rank, the number of homophones given a lexicon, and the number of possible part-of-speech tags for the hypothesized word.
Error detection
As introduced in [1], a confidence measure, p, is estimated from a feature vector 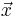 using a generalized linear model:
using a generalized linear model:
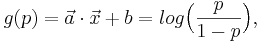
g is a monotonic function, called the link function. Vectors
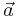 and b are the parameters of the model estimated
under the maximum likelihood criterion.
and b are the parameters of the model estimated
under the maximum likelihood criterion.
- The logit link function is used (logistic regression).
- Results are evaluated using the classification error rate (CER).
- To set up the baseline result, we may assume that the most likely words given by the confusion network are always correct.
Corpus and ASR system
The data set is the official test of the French ester campaign: 10 hours of recent French radio broadcast news shows (107k words). As described in [6], LIMSI's French real-time transcription system is used (two pass decoding using a vocabulary of 65k words and words, interpolated n-gram back-off LM). In the following table is reported a summary of the generated data. Two sub-categories are distinguished, whether the best posterior probability of the CS (post) is lower or greater than 0.95.
| Data set | Total | Errors | Error rate |
|---|---|---|---|
| All data | 107602 | 18472 | 17.2 |
post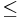 0.95 0.95
|
57823 | 16150 | 27.9 |
| post>0.95 | 49779 | 2322 | 4.7 |
Table 1
Experiments
Results obtained with various combination of feature types show that the use of features based on language model or lexical resources does not result in a great improvement. We may assume that informations carried by these models are already used by the speech decoder. On the contrary, the use of features solely extracted from the confusion networks yields to a significant improvement. The CER is reduced by a quarter when using only the following features: the best posterior probability, the local entropy, the number of parallel edges, the duration and the length of the hypothesized word. This relative gain raises to 27% by adding the "contextual" features (null edge as hypothesized word in the left or right CS, and the length of the confusion network).
The impact of each feature may be sorted by ranking their associated t-values. This measure is the ratio of the estimated parameter value to its standard error. From this ranking can be inferred that the greatest predictor is the best posterior probability as expected. The following predictors are in decreasing order, the local entropy, duration, and the number of parallel edges. The impact of other features are less significant.
A cross evaluation is performed to assess the impact of partitioning
the data depending on post: two logistic regression models
are estimated on each training corpus and tested on both test corpus.
Results are given in table 2. When looking at the
first column, it can be inferred that training the classifier on data
with post > 0.95 to classify data with post 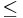 0.95 performs poorly to be compared with the classifier trained on
data with post
0.95 performs poorly to be compared with the classifier trained on
data with post 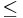 0.95 (a CER of 29.1% vs
19.9%). Nevertheless, merging all training data to classify data
with post
0.95 (a CER of 29.1% vs
19.9%). Nevertheless, merging all training data to classify data
with post 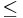 0.95 does not impoverish the CER. It
can also be observed that whatever the training set, the CER still
quite identical to the baseline one, when testing on data with
post
0.95 does not impoverish the CER. It
can also be observed that whatever the training set, the CER still
quite identical to the baseline one, when testing on data with
post 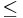 0.95. Thus an appropriate decision rule to classify
this kind of CS may be simply to decide that the ASR system is still
right. These results confirm the assumption of~\cite{hillard06} and
justify the partitioning of the data.
0.95. Thus an appropriate decision rule to classify
this kind of CS may be simply to decide that the ASR system is still
right. These results confirm the assumption of~\cite{hillard06} and
justify the partitioning of the data.
| Training set / test set | post 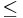 0.95 0.95 |
post>0.95 |
|---|---|---|
post 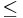 0.95 0.95
|
19.9 | 4.9 |
| post>0.95 | 29.1 | 4.5 |
Table 2: Cross evaluation with the different data partitions: for each part of
the training
data a regression model is trained and evaluated on each test corpus.
Our best system for confidence estimation and error detection is
obtained as follow: the training data corresponding in a post
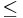 0.95 are used to estimate a logistic regression model using all
the features described in this article, including the features from
adjacent sets. This model is used to estimate the correctness
probability of CSs with a post
0.95 are used to estimate a logistic regression model using all
the features described in this article, including the features from
adjacent sets. This model is used to estimate the correctness
probability of CSs with a post 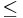 0.95. For the other
CSs, the ASR system is assumed to always hypothesize the right
word. With this approach, our system achieve a CER of 12.3% on the
whole test set of 20k confusion sets. This represents a relative
reduction of 28.5%.
0.95. For the other
CSs, the ASR system is assumed to always hypothesize the right
word. With this approach, our system achieve a CER of 12.3% on the
whole test set of 20k confusion sets. This represents a relative
reduction of 28.5%.
References
[1] L. Gillick, Y. Ito, and J. Young, “A probabilistic approach to confidence estimation and evaluation,” in Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, vol. 2, Munich, Germany, 1997, pp. 879–882.
[2] D. Hillard and M. Ostendorf, “Compensating for word posterior estimation bias in confusion networks,” in Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Toulouse, France, May 2006.
[3] M. Weintraub, F. Beaufays, Z. Rivlin, Y. Konig, and A. Stolcke, “Neural-network based measures of confidence for word recognition,” in Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 1997, pp. 887–890.
[4] L. Mangu, E. Brill, and A. Stolcke, “Finding consensus in speech recognition: Word error minimization and other applications of confusion networks,” Computer, Speech and Language, vol. 14, no. 4, pp. 373–400, 2000.
[5] T. Kemp and T. Schaaf, “Estimating confidence using word lattices,” in Proc. Eurospeech ’97, Rhodes, Greece, 1997, pp. 827–830. [Online]. Available: citeseer. ist.psu.edu/kemp97estimating.html
[6] J.-L. Gauvain, G. Adda, M. Adda-Decker, A. Allauzen, V. Gendner, L. Lamel, and H. Schwenk, “Where Are We in Transcribing French Broadcast News?” in InterSpeech, Lisbon, September 2005.