Thermodynamics of the multi-cellular transition for natural convection in tall cavities

M. Pons

Objectives

Natural convection in cavities with large aspect ratio (Height/Width) has been investigated for long. Nevertheless, it receives renewed interest. We develop herein a thermodynamic approach of the transition from the mono-cellular conduction regime to the multi-cellular regime. This problem is exemplified with air in a cavity of aspect ratio A=20. The purpose is twofold. First, we investigate how the work of pressure forces modifies the results and we evidence its effects in configurations that belong to daily life. Second, we highlight how relevant thermodynamic quantities are modified by the transition.

Description

Following Spiegel & Veronis (1960), the Boussinesq model is modified into the thermodynamic Boussinesq model that accounts for, first and more importantly, the work of pressure forces, second and just for sake of thermodynamic consistency, the heat generated by viscous friction (see our previous Scientific Reports). Now, each configuration is described by the Rayleigh number Ra AND the parameter φ, which is the adiabatic temperature gradient non-dimensionalized in the problem framework:
.
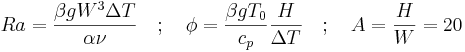Two cavities with given heights are considered herein: a small one, where the work of pressure stress is negligible (φ much less than 1, like in the usual Boussinesq model), and a large one where that work is not negligible (φ of the order of 1). The two cavities are described in the Table here-under, where the values of φ and ΔT are those corresponding to Ra=5000. Values of Ra above 5000 are obtained by increasing ΔT, so that φ is meanwhile decreased proportionally. Note that both cavities are of human size, not of geophysics dimensions.

Results

Effect of pressure work

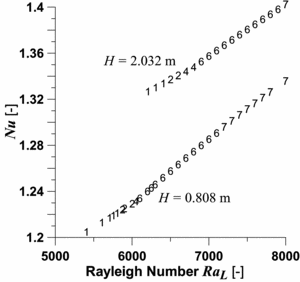
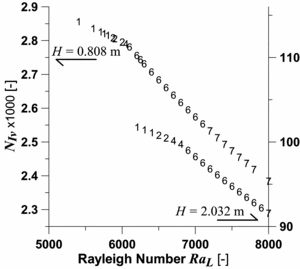
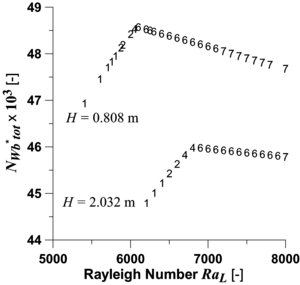
The Figures 1 and 2 respectively present the Nusselt number and the number of viscous irreversibility 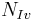versus the Rayleigh number. As 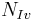is scaled by the factor φ (see Pons & Le Quéré 2007), for sake of comparison the scales of the ordinate axes in Figure 2 are in the same ratio as the respective values of φ: 40.

Figure 1: Nusselt number for both cavities. Numbers indicate the number of cells (1: mono-cellular flow, 2: two secondary cells, etc.)

Figure 2: Number of viscous irreversibility scaled for direct comparison (left Y-axis for the small cavity, right Y-axis for the large one). Same convention as in Fig. 1.

It first can be seen that the differences between the two configurations are not negligible. Compared to the small cavity, the Nusselt in the large cavity is 6% larger although convection is less intense. Accurate analysis shows that 20% of the total heat transfer in the large cavity is due to the work of pressure forces. Such results demonstrate that this effect is not negligible in volumes that are very common in buildings. Moreover, as the pressure work effect reduces convection, it delays the transition from mono-cellular to multi-cellular flow (Ra around 6800 instead of 6000).

Analysis of transition

According to stability analyses based on the usual Boussinesq equations, the critical Rayleigh number, 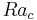, lies between 5600 and 5700 (Vest and Arpaci 1969, Bergholz 1978). We observe two secondary cells in the small cavity for Ra=5875 (and Ra=6500 in the large one).
However, if each curve in Figures 1 and 2 does make a knee, this knee is not located at the transition between one and two cells, but at that from 4 to 6 cells. Is the velocity field alone sufficient for describing the transition phenomenon?
It also can be seen that the onset of multi-cellular flow relatively increases heat transfer (i.e. the slopes in Figure 1 are larger after transition than before) while relatively decreasing convection and viscous friction (see Figure 2). How do the secondary cells altogether decrease viscous friction and increase heat transfer?

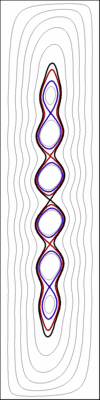
Figure 3: Velocity field with six secondary cells

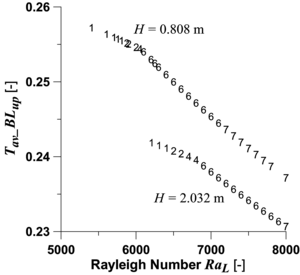
Figure 3 shows that, instead of forming a row, the secondary cells (co-rotative) are actually imbricated in successive levels: the flow first decomposes into two cells only (black streamline), each of them then decomposes into two other ones (red streamline), and so forth until the deepest level (blue streamline). As a consequence, each individual secondary cell undergoes friction with only one neighboring cell while being carried around on the other side by the cell of the upper level. This topology obviously offers less resistance. On another hand, the secondary cells induce local recirculation and undulations of the primary flow. Both phenomena locally increase conductive heat flux. This is how the Nusselt number is relatively increased (see Figure 1). Moreover, this local heat flux also tends to modify the average temperature in either boundary layer: increased temperature in the cold boundary layer, reduced in the hot one (see Figure 4). The temperature changes in the boundary layers induced by the transition have another consequence: the buoyancy forces, and the mechanical work they generate, are reduced. Figure 5, which presents this mechanical work for the different configurations, very clearly exhibits the transition between 4 and 6 cells. This mechanical work is the engine of natural convection. This remark leads to a thermodynamic explanation of the threshold. The secondary cells appear when the shear along the centerline of the cavity is strong enough, like in the Kelvin-Helmholtz instability, i.e. when convection is strong enough. Once they appear, the secondary cells simultaneously induce two phenomena: first, decrease of viscous friction (rolls resist less than shear along a line), second, reduction of the mechanical work generated by the buoyancy forces (consistently with the reduced viscous friction), via a reduction of the temperature difference between the two boundary layers (which results in an increased heat transfer). A reduced mechanical work means a less intense convection. In other words, when they appear, the secondary cells weaken their own source: this is the reason why a threshold exists, and there is no trend to maximize heat transfer.

Figure 4: Average temperature in the hot boundary layer.

Figure 5: Work of the buoyancy forces.

Conclusions

The work of pressure forces is not negligible in configurations that can easily be met in building engineering (2-3m high). For simulating such cases, the Boussinesq model must be corrected.
Thermodynamics give valuable insight into the phenomena involved in thermoconvective transitions.

References

Bergholz, R. F., 1978, Instability of steady natural convection in a vertical fluid layer, J. Fluid Mech., 84, 743-768.
Pons, M. and P. Le Quéré, 2007, Modeling natural convection with the work of pressure-forces: a thermodynamic necessity, Int. J. Numer. Methods Heat Fluid Flow, 17, 322-332.
Spiegel, E. A. and G. Veronis, 1960, On the Boussinesq approximation for a compressible fluid, Astrophys. J, 131, 442-447.
Vest, C. M. and V. S. Arpaci, 1969, Stability of natural convection in a vertical slot, J. Fluid Mech. , 36, 1-15.

Links