TSF: gas storage
Contents |
Influence of the inlet flow on the development of velocity for saturated porous media
Objectives
Storing hydrogen is a key point for the development of environment-friendly vehicles. Modelling a hydrogen tank with active carbon requires some simplifying assumptions. Our concern is to evaluate the validity of one of those assumptions: the nonhomogeneities of the flow at the bed entry vanish after covering a distance inside the bed. We evaluate this distance for different values of the governing parameters that are the Reynolds number, the Darcy number, the Forchheimer effects and the geometry of the reservoir entry.
Description
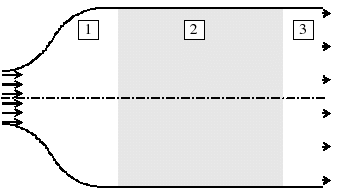
The reservoir is axisymetric and divided in three regions as presented in figure 1: 1/ the fluid volume (diameter 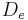 and length
and length 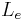 ) separating the entry of the reservoir and the active carbon bed, 2/ the granular bed (diameter
) separating the entry of the reservoir and the active carbon bed, 2/ the granular bed (diameter 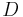 and length
and length 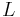 ), 3/ the outflow region (diameter
), 3/ the outflow region (diameter 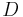 and length
and length 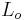 ). The unsteady Navier Stokes equations for incompressible flow are solved in axisymmetric 2D coordinates simultaneously in the fluid region and in the porous bed. The calculations are stopped when steady state is reached. In the porous region, a Darcy-Forchheimer relation between pressure gradient and velocity is utilized as a penalty term. Different upstream conditions are studied depending on the values of the diameter
). The unsteady Navier Stokes equations for incompressible flow are solved in axisymmetric 2D coordinates simultaneously in the fluid region and in the porous bed. The calculations are stopped when steady state is reached. In the porous region, a Darcy-Forchheimer relation between pressure gradient and velocity is utilized as a penalty term. Different upstream conditions are studied depending on the values of the diameter 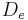 and length
and length 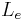 . When
. When 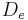 is small, the flow rate at the reservoir entry is high. The geometrical characteristics of the reservoir are:
is small, the flow rate at the reservoir entry is high. The geometrical characteristics of the reservoir are: 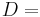 96mm,
96mm,
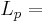 288mm. Three values of the entry diameter and four values of the entry length have been investigated:
288mm. Three values of the entry diameter and four values of the entry length have been investigated: 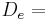 6, 12, or 24mm and
6, 12, or 24mm and 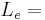 6, 12, 24, or 48mm. The reservoir diameter
6, 12, 24, or 48mm. The reservoir diameter 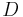 and the out-flow velocity
and the out-flow velocity 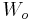 were chosen as the cheracteristic length and velocity. We study the development of the velocity field in the reservoir. At each axial position of the bed, velocity is maximal on the axis. Then we state that the flow is uniform across a given section of the bed when the velocity on the center point of this section is less than 1.05
were chosen as the cheracteristic length and velocity. We study the development of the velocity field in the reservoir. At each axial position of the bed, velocity is maximal on the axis. Then we state that the flow is uniform across a given section of the bed when the velocity on the center point of this section is less than 1.05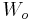 . Along the distance between the bed entry and this section the flow is set non homogeneous, and this distance is called "length of stabilization" of the fluid flow through the porous bed.
. Along the distance between the bed entry and this section the flow is set non homogeneous, and this distance is called "length of stabilization" of the fluid flow through the porous bed.
When the gas inflow is low, the flow in the entry section is laminar and the fluid reaches the bed entry section with quasi uniform velocity. In this case the flow has forgotten its inlet conditions. In such configurations, discarding a detail simulation of the fluid flow inside the entry region will not affect the fluid motion through the porous bed. When the gas inflow is high, or if the distance between the entry and bed is short, the flow arriving to the bed entry section is not homogeneous and still marked by the inflow conditions. For example the jet can reach directly the bed entry section and the velocity will be more important near the axis of the reservoir than near its periphery. The fluid velocity in the bed will be homogeneised only after a given distance in the bed.
Results and Discussion
Effects of Forchheimer term
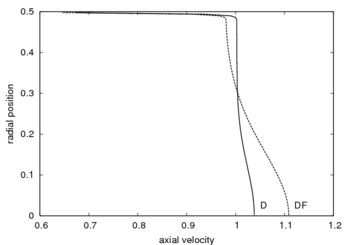
We performed a study to show the variation between two different models (Darcy and Darcy-Forchheimer) by comparing the corresponding difference in velocity and depth of stabilization of the fluid flow. The controlling parameters used are porosity, inertia parameter, Darcy number and Reynolds number. For the case of Darcy numbers corresponding to practical applications, the two models are found to result in velocity fields which are close to each other for a given porosity or inertia parameter. The axial velocity profiles presented on the figures 2a and 2b correspond to two cases where the inertial quadratic velocity term is taking into account or dropped. The calculations were done for the same Darcy number 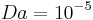 , and for different values of the Reynolds number and entry diameters. The figure 2a corresponds to the following parameters:
, and for different values of the Reynolds number and entry diameters. The figure 2a corresponds to the following parameters: 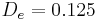 (
(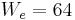 ),
), 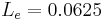 ,
, 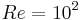 . The velocities on the axis are respectively
. The velocities on the axis are respectively 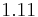 (Darcy-Forchheimer) and
(Darcy-Forchheimer) and 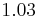 (Darcy). We notice that the difference is about 7%. The figure 2b corresponds to
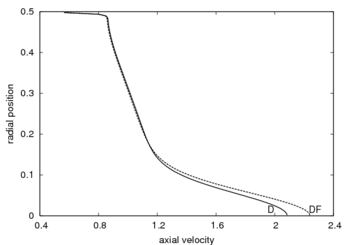
(Darcy). We notice that the difference is about 7%. The figure 2b corresponds to 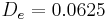 (
(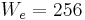 ),
), 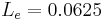 ,
, 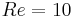 . The velocities on the axis are respectively
. The velocities on the axis are respectively 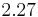 (Darcy-Forchheimer) and
(Darcy-Forchheimer) and 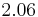 (Darcy). We notice that the difference is about 9%. The numerical results confirm that the maximum value of the velocity is located on the axis.
(Darcy). We notice that the difference is about 9%. The numerical results confirm that the maximum value of the velocity is located on the axis.
Influence of the length of the entry region
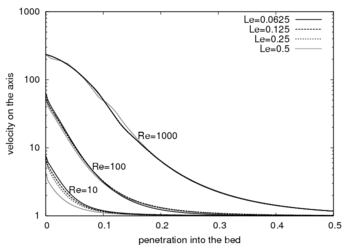
The figure 3 presents the evolution of the velocity on the axis as a function of the penetration into the bed. The computations have been done for an entry diameter 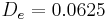 (
(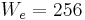 ) and a Darcy number
) and a Darcy number 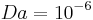 . The figure 3 shows that the heterogeneity of the flow decreases strongly into the bed. In the extreme case when the Reynolds number
. The figure 3 shows that the heterogeneity of the flow decreases strongly into the bed. In the extreme case when the Reynolds number 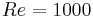 , this heterogeneity concerns a length of
, this heterogeneity concerns a length of 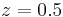 . We have investigated three values of the Reynolds number
. We have investigated three values of the Reynolds number 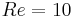 ,
, 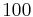 , and
, and 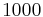 . The numerical simulations show that the axial velocity in the bed is practically the same for four different values of the length entry:
. The numerical simulations show that the axial velocity in the bed is practically the same for four different values of the length entry: 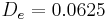 ,
, 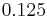 ,
, 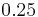 , and
, and 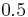 when the reservoir entry diameter is equal to 0.0625. We conclude that for small entry diameters, the velocity profiles are practically the same and are then independent of the entry length which denotes the distance between the reservoir entry and the granular bed. This distance can be taken small in order to reduce the price of the reservoir. When the entry diameter equals 0.0625 the thicknesses needed for the homogeneisation of the flow in the bed are 0.1, 0.25 and 0.5 when the Reynolds number is respectively equal to 10, 100 and 1000. This is the response to the question of the validity of a simplified hypothesis of homogeneous flow all over the bed.
when the reservoir entry diameter is equal to 0.0625. We conclude that for small entry diameters, the velocity profiles are practically the same and are then independent of the entry length which denotes the distance between the reservoir entry and the granular bed. This distance can be taken small in order to reduce the price of the reservoir. When the entry diameter equals 0.0625 the thicknesses needed for the homogeneisation of the flow in the bed are 0.1, 0.25 and 0.5 when the Reynolds number is respectively equal to 10, 100 and 1000. This is the response to the question of the validity of a simplified hypothesis of homogeneous flow all over the bed.
Conclusion
The homogeneization of the flow is governed by the product of the Reynolds and Darcy numbers. When the reservoir has a small entry diameter the thickness of the bed needed for the homogenization of the flow in the bed is small. The simplifying assumption of validity of the Darcy low trough the bed is verified. We can affirm that the flow is homogeneous in the bed after a thickness which equals half its diameter. This was verified for 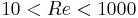 and
and 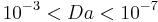 . Usually the length of reservoirs equals 5 to 10 times its diameter.
. Usually the length of reservoirs equals 5 to 10 times its diameter.