Control at the wall of turbulent flows
L. Lorang-Vo Dinh, G. Fournier, B. Podvin, P. Le Quéré, S. Pellerin and L. Ta Phuoc
Contents |
Object
Control of turbulence represents one of the major directions of current fluids research. Turbulent flows are characterized by complex dynamics and a large range of scales, which makes them difficult to compute. A wide variety of applications exists for this theoretically challenging issue, ranging from enhanced mixing in the pharmaceutical industry to drag reduction over aircrafts and ships. The focus of this group is to build on our experience with numerical simulations (both direct and LES) of turbulent flows to experiment with flow control techniques. Numerical simulation provides a unique, idealized setting frame in which 1) a wide range of control parameters can be explored easily 2) the effect of a given control on the flow can be entirely determined in space and time. Simulating manipulated flows therefore constitutes a first step towards the validation of control. The insight obtained with artificial control in numerical simulations can then be confronted with experiments to develop a realistic control strategy. This approach has been carried out at LIMSI for both free-shear (wake of bluff bodies) and wall-bounded flows. In all cases the flow-dependent manipulation technique consisted in blowing and sucking at the flow boundary.
Turbulence at the wall
Our goal is to develop new control strategies for drag reduction in a turbulent channel. Specifically, the idea is to determine instantaneous key features of wall turbulence using accessible data such as wall shear measurements. Our approach is based on the POD technique coupled with neural networks. Neural networks are excellent tools to estimate a non-linear dynamical process from observable data. The method is first tested in a turbulent channel of relatively small horizontal dimensions, then in a larger channel. In both cases estimation and control are performed on subdomains of relatively small dimensions.
Bluff bodies
The turbulent separated flows past several bluff bodies, i.e. a circular cylinder, the
Malavard-Cousteau's Turbosail and a NACA0012 airfoil, are computed by using
Large Eddy Simulations (LES). In order to modify the aerodynamic coefficients of
the circular cylinder, a boundary layer suction is applied at the wall of the body.
Moderate Reynolds numbers less than 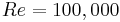 are considered in this study, corresponding to the subcritical
regime (laminar separation of the boundary layer).
Comparisons with experimental studies carried on in LEA/ENSMA
(Poitiers, France) are shown for the flow around a circular cylinder, at a high Reynolds number
are considered in this study, corresponding to the subcritical
regime (laminar separation of the boundary layer).
Comparisons with experimental studies carried on in LEA/ENSMA
(Poitiers, France) are shown for the flow around a circular cylinder, at a high Reynolds number 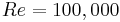 .
The control efficiency on lift enhancement and drag reduction is analyzed for the turbosail and NACA profiles
as function of the angle of incidence. The suction modifies also the topology of the flow.
.
The control efficiency on lift enhancement and drag reduction is analyzed for the turbosail and NACA profiles
as function of the angle of incidence. The suction modifies also the topology of the flow.
Blowing and suction at the wall of a turbulent channel using neural networks
Control strategy
The control strategy is similar to the one described by Lee et al. (1997). This neural network aims to find a correlation between wall-shear stress and wall actuations from given data sets. We only use the transverse wall-shear stress 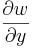 as the adding of
as the adding of 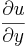 was not relevant for the neural network performance. The desired wall actuations is the one recommended by Choi et al. [2] i.e. the opposite of the velocity at
was not relevant for the neural network performance. The desired wall actuations is the one recommended by Choi et al. [2] i.e. the opposite of the velocity at 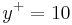 (Fig. 1). This strategy of blowing and suction at the wall brings about a drag reduction of 25% by reducing the sweep and ejection events in the wall-layer.
(Fig. 1). This strategy of blowing and suction at the wall brings about a drag reduction of 25% by reducing the sweep and ejection events in the wall-layer.
Finally, the flow around a thin wing profile (NACA0012) for 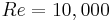 is considered.
The suction is here applied on a surface of 12 % of the chord, starting close to the upstream stagnation point,
with a suction velocity ten times smaller than the upstream velocity.
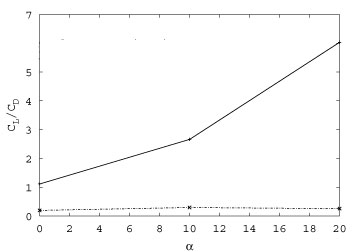
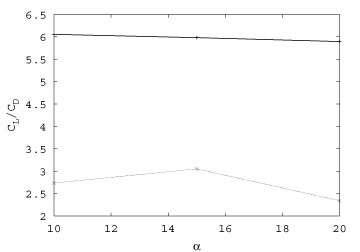
On the opposite of the Turbosail, the NACA0012 has a great lift-on-drag ratio even when no suction occurs. Nevertheless,
the suction is able to raise this ratio up to very high values, proving that this kind of control techniques is not only able to create a lift force, but also to enhance it (Figure 4).
is considered.
The suction is here applied on a surface of 12 % of the chord, starting close to the upstream stagnation point,
with a suction velocity ten times smaller than the upstream velocity.
On the opposite of the Turbosail, the NACA0012 has a great lift-on-drag ratio even when no suction occurs. Nevertheless,
the suction is able to raise this ratio up to very high values, proving that this kind of control techniques is not only able to create a lift force, but also to enhance it (Figure 4).
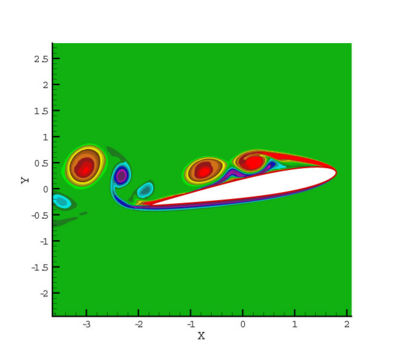
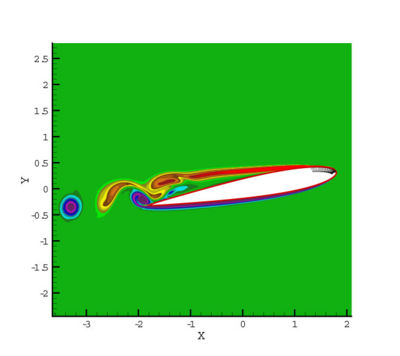
In addition to the efficiency improvement, the suction can also greatly modify the flow patterns, such as the vortex shedding. Indeed, it can be observed on Figure 5 that when a suction is applied, the shed vortex are smaller than they would be in the uncontrolled case.
The main reason is that the boundary layer separation is delayed by the suction. The wake thickness and consequently
the typical size of the vortex are then reduced.
The control influences then also the vortex frequency. In the case of the uncontrolled flow, two kind of vortices are generated, at both attack (boundary layer separation) and leading edges (Figure 5.a). The resulting shed vortex has a mixed frequency. In the case of control, vortices are only created at the leading edge of the profile (Figure 5.b). The resulting frequency corresponds then to the leading edge frequency, higher than the initial one.
Discussion and conclusion
Neural networks and turbulence at the wall
In this work, we have tried to control the flow near the wall of a boundary-layer by the means of two approaches: Neural networks and POD analysis. By combining the two approaches, we hope we could develop new strategies for drag minimization using realistic wall measurements. These results underline the complex influence of a wide variety of organized motions in the turbulence generation process. Practical impediments need to be adressed as well as theoretical issues to make a control strategy successful. Up to 13% reduction was obtained when only wall information was used, while full flow information resulted in 20%. The performance of Fourier based neural networks is comparable to those derived in physical space (15% for Lee, Babcock and Goodman), while requiring handling very little information.
Bluff bodies and LES at high Reynolds number
Two main conclusions can be drawn about this study. First, the ability of Large Eddy Simulations to predict high Reynolds number separated turbulent flows has been proved by means of comparisons with experimental results (LEA/ENSMA), even if a control by suction is applied. The control by boundary layer suction has then been shown to be of great interest to modify the aerodynamic coefficients, either for a bluff body or for an airfoil. Moreover, the suction can also strongly modify the vortex shedding pattern and appear to be a good method to reduce Vortex-induced Vibrations on airplane wings for instance.
Several other means of control have to be checked in the future, mainly synthetic jets which are known to be rather efficient as a flow control technique, consisting of a half-period suction followed by a half-period blowing to ensure that there will be no net mass injection in the flow. In addition, because of the high Reynolds number considered here, the influence of the suction in the spanwise direction might also be investigated.
This study is part of Guillaume Fournier's PhD Thesis (2005).
References
- Lardat (1997) Simulations numériques d'écoulements externes instationnaires décollés autour d'une aile avec des modèles de sous-maille, PhD Thesis, Université Pierre et Marie Curie - Paris VI.
- Ta Phuoc (1994) Modèles de sous-maille appliqués aux écoulements instationnaires et décollés, Journée Thématique DRET, Paris.
- Fournier (2005) Contrôle de l'écoulement décollé autour de profils épais par la Simulation des Grandes Echelles, PhD Thesis, Université Pierre et Marie Curie - Paris VI.
- Lee, Kim, Babcock and Goodman (1997) Application of neural networks to turbulence control for drag reduction, Physics of Fluids, Vol. 9, No 6, pp. 1740-1747.
- Choi, Moin and Kim (1994) Active turbulence control for drag reduction in wall-bounded flows, J. of Fluid Mech., Vol. 262, pp. 75-110.
- Lorang Vodinh, Podvin, Le Quéré (2005) Flow estimation using neural network, Turbulence and Shear Flow Phenomena, 27-27 June 2005 , Williamsburg, VA USA.
- Lorang (2007) Contrôle de la traînée dans la zone de paroi d'un canal plan turbulent à l'aide de réseaux de neurones, PhD Thesis, Université Pierre et Marie Curie - Paris VI.
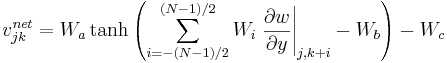 (1)
(1)
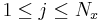 and
and 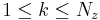
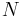 is the number of neighbouring points in the spanwise direction.
is the number of neighbouring points in the spanwise direction. 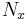 and
and
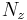 are respectively the number of gridpoints in the streamwise direction and in the spanwise direction.
The
are respectively the number of gridpoints in the streamwise direction and in the spanwise direction.
The 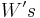 are the weights of the neural network that are established during a learning process. This learning process is based on a simplex algorithm used to train the neural network obtaining the desired Choi actuation by minimising the error defined in (2),
where
are the weights of the neural network that are established during a learning process. This learning process is based on a simplex algorithm used to train the neural network obtaining the desired Choi actuation by minimising the error defined in (2),
where 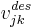 represents sets of Choi's wall velocity field.
represents sets of Choi's wall velocity field.
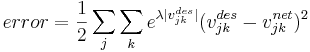 (2)
(2)
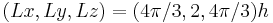 , and a grid resolution of (96,65,48). The Reynolds number based on the channel half-height
, and a grid resolution of (96,65,48). The Reynolds number based on the channel half-height 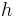 and center line velocity is 4000 and the one based on
and center line velocity is 4000 and the one based on 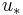 is about 140.
is about 140.
 ), we observe the correlation between the extracted velocity and wall shear stress. Let us call
), we observe the correlation between the extracted velocity and wall shear stress. Let us call
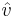 the projection of normal velocity onto the first eigenfunction of the uncontrolled flow.
The resulting curves revealed that
the projection of normal velocity onto the first eigenfunction of the uncontrolled flow.
The resulting curves revealed that 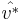 and
and 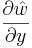 were well correlated in the uncontrolled flow. The relation can be written as:
were well correlated in the uncontrolled flow. The relation can be written as:
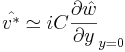 (3)
(3)

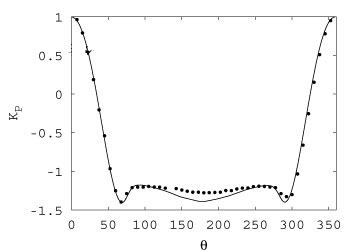
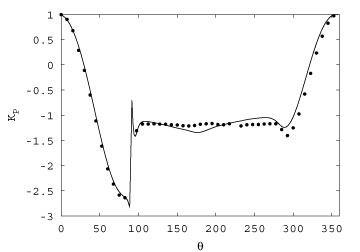
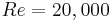 . This bluff body
was created by Malavard and Cousteau in order to create a new wind-powered boat, named Alcyone, to replace the old Calypso.
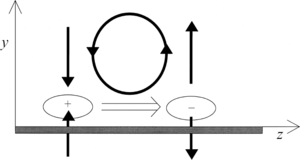
The Turbosail, an ovoid-section cylinder acts exactly like a sail, the lift force being created by a huge fan, located in the cylinder,
and sucking the flow through a permeable wall (Figure 2). In this study, the suction velocity is ten times smaller than the upstream
velocity and the suction surface, beginning at about 45 % of the profile chord, spreads over 26 % of the chord.
. This bluff body
was created by Malavard and Cousteau in order to create a new wind-powered boat, named Alcyone, to replace the old Calypso.
The Turbosail, an ovoid-section cylinder acts exactly like a sail, the lift force being created by a huge fan, located in the cylinder,
and sucking the flow through a permeable wall (Figure 2). In this study, the suction velocity is ten times smaller than the upstream
velocity and the suction surface, beginning at about 45 % of the profile chord, spreads over 26 % of the chord.