Unsteady flow dynamics through the glottis for vocal production modeling
D. Sciamarella and P. Le Quéré in collaboration with G. Artana (Univ. de Buenos Aires)
Contents |
Object
A better comprehension of voice generation in humans is essential for the development of vocal fold models which can be integrated in voice synthesis applications. Besides, deterministic physical models of voice production give access to the physiological parameters needed in medical applications and help sorting out, among the acoustic properties of sound signals, those under direct neural control from those being purely biomechanical.
Voiced sounds are produced by the pulsatile flow generated during the self-sustained oscillations of the vocal folds. Pulsatile flow with flow separation is a very general problem in fluid mechanics. The purpose of our work is to build on previous efforts to provide an accurate description of the physics of this phenomenon, in order to construct less caricatural models of glottal flow, and therefore improve the acoustic quality of the predicted sound.
Among these issues, the characterization of the dynamic development of the airflow within the glottal channel is essential to improve the standard flow portrait adopted by low-order conventional vocal-fold models. Such models do not properly account for flow separation near the glottal outlet or for turbulent dissipation of kinetic energy in the glottal jet, and consequently disregard the main volume-control effect, along with its acoustic correlate.
Description
The soft tissues in the glottis are not only subject to the action of muscular forces but also to the pressure forces of the air passing through. Vocal folds are membranes which periodically open and close the glottal duct, driven by the fluid-structure energy transfer. The glottal channel has therefore a constriction (delimited by the vocal folds) which is convergent in the opening phase, and divergent in the closing phase. The physics of the phenomenon involves two particularly difficult questions, namely, the evolution of glottal flow during vocal fold collision and turbulent flow separation around the glottal exit.
These aspects of phonation mechanics exceed the caricature of glottal flow adopted in low-order vocal-fold models [Pelorson et al, 1994]. Such models are extremely useful because they provide a simple and powerful description of the basic mechanisms of voiced sound generation in humans [Sciamarella et al, 1999], primates [Herzel et al, 2006] or songbirds [Sciamarella et al, 2006]; in fact, they capture a wide range of phenomena (register transitions, vibrato, diplophonia, biphonation, etc) [Lucero, 2005] particularly interesting for speech synthesis [Sciamarella et al, 2005]. Flow effects are incorporated to such models under the form of ad hoc criteria [Lous et al, 1998]. Nevertheless the available criteria predict the forces acting on the vocal folds with errors of 100% [Ruty et al, 2005]. In view of the acoustic relevance of these issues for voice synthesis, assessed in [Sciamarella, 2004], it is clear that further research is necessary.
In order to cope with these difficulties, the strategy is to unfold the triptych: numerical simulation / experimental data / modeling, in the specific case of the airflow traversing a phonating glottis. For our simulation purposes, we have implemented an incompressible Navier-Stokes solver with a multigrid finite-difference method and moving immersed boundaries, which is different from previous approaches in its numerical scheme (lower computational cost and guarantee of unaltered accuracy), but also in the possibility of admitting different conditions for the entrance flow (e.g. constant or time-dependent inflow). Numerical experiments have been performed focusing mainly on the variability in the mobility of flow detachment from the moving walls representing the vocal folds (see Fig.1) [Sciamarella, 2007].
The experimental counterpart of the triptych is based on the setups with human vocal fold replica studied by X. Pelorson and coworkers (ICP, Grenoble), which allow for two types of dynamical measurements: pressure and geometry. In order to achieve measurements of the flow field, flow visualization in in-vitro models of the glottal channel is being projected at the Laboratorio de Fuidodinamica (LFD, Buenos Aires, Argentina) in collaboration with G. Artana.
Results
Furthermore, numerical experiments show that the explanation of inertial forces retarding flow effects with respect to wall motion is not pervasive either. Whether it is clear that geometric criteria should be abandoned in favor of a dynamical criterion, simulations show that identifying the conditions that systematically control reversal of intraglottal flow will not be a simple task, in particular due to the sensitivity to boundary conditions, which remain conjectural to some extent.
On the other hand, flow instabilities past the constriction (which prevent flow solutions from achieving a steady state) do not seem to affect flow behavior within the glottal constriction, that remains periodical with the frequency of the forced oscillations.
Prospects
The implemented numerical solver is currently being applied to alternative channel geometries, corresponding to the in-vitro tests performed in Grenoble, which are conceived to assess the influence of false vocal folds in phonation. On the other hand, we expect to obtain interesting data from flow visualizations [Arnaud et al, 2006] in experimental setups specifically designed to match the conditions imposed in our numerical experiments. Last but not least, it is worth noting that realistic vocal fold motion (which includes a colliding phase) considerably strains the numerical stability of the flow solver in the absence of a suitable inflow boundary condition. In order to overcome this hindrance, the numerical algorithm could be improved defining, for instance, two separate computational domains for the subglottal and supraglottal regions during collision, at the expense of introducing certain complementary assumptions, which are likely to be available from the experimental essays we project. Incorporating fluid-structure interaction to the flow solver is another fundamental pending issue of our program.
References
[Arnaud et al, 2006] E. Arnaud, E. Mémin, R. Sosa, G. Artana. A Fluid Motion Estimator for Schlieren Image Velocimetry. Lecture Notes in Computer Sciences, 3951/2006, pp. 198-210.
[Lous et al, 1998] N. Lous, G.C.Hofmans, R. Veldhuis, A. Hirschberg, A symmetrical two-mass vocal-fold model coupled to vocal tract and trachea, with application to prosthesis design, Acta Acustica 84 (1998) 1135–1150.
[Lucero, 2005] Jorge C. Lucero. Bifurcations and limit cycles in a model for a vocal fold oscillator. Communications in Mathematical Sciences, 3:517–529, 2005.
[Herzel, 2006] Hans-Peter Herzel, R. Zaccarelli, T. Riede, J. Neubauer, and W. Tecumseh Fitch. Nonlinear phenomena in vertebrate vocal production, J. Acoust. Soc. Am. 120, 3189 (2006)
[Pelorson et al, 1994] X. Pelorson, A. Hirschberg, R. R. van Hassel, A. Wijnands, Y. Auregan, Theoretical and experimental study of quasi-steady flow separation within the glottis during phonation. Application to a modified two-mass model., J. Acoust. Soc. Am. 96 (1994) 3416–3431.
[Ruty et al, 2005] N. Ruty, A. van Hirtum, X. Pelorson, I. Lopez & A. Hirschberg. A mechanical experimental setup to simulate vocal folds vibrations. Preliminary results. ZAS Papers in Linguistics 40, 2005: 161-175
[Sciamarella et al, 1999] D. Sciamarella, G. B. Mindlin, Topological Structure of Flows from Human Speech Data. Physical Review Letters 82, 7 (1999)
[Sciamarella, 2004] D. Sciamarella, C. d’Alessandro, On the acoustic sensitivity of a symmetrical two-mass model of the vocal folds to the variation of control parameters, Acta Acustica 90 (2004) 746–761.
[Sciamarella et al, 2005] D. Sciamarella, C. D’Alessandro. Stylization of glottal-flow spectra produced by a mechanical vocal-fold model, Proc. of Interspeech 2005, pp 2149
[Sciamarella et al, 2006] D. Sciamarella, R. Laje, G. B. Mindlin, Comportement des sources acoustiques couplées dans un modèle du syrinx des oscines, Notes et Documents du LIMSI 2006-16 (2006)
[Sciamarella et al, 2007] D. Sciamarella, P. Le Quéré, Solving for unsteady airflow in a glottal model with immersed moving boundaries, European Journal of Mechanics B/Fluids (2007), doi:10.1016/j.euromechflu.2007.06.004
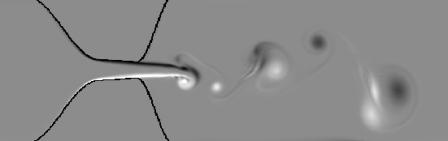
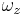 ) across the glottal channel in the opening phase of the vocal-fold cycle.
) across the glottal channel in the opening phase of the vocal-fold cycle.
 (pluses) and glottal half-angles
(pluses) and glottal half-angles 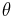 (full line) for a phonating glottis (Re=2000), compared with the locations (dashed line) predicted by quasi-static criteria.
(full line) for a phonating glottis (Re=2000), compared with the locations (dashed line) predicted by quasi-static criteria.