Stability of the flow between two exactly counter-rotating disks with large aspect ratio
Martin Witkowski L, Nore C, Delbende I, Le Quéré P, Daube O
In collaboration with Walker J.S (Urbana Champaign, USA), Foucault E, Pécheux J (LEA, Poitiers).
Contents |
Object
The flow between two parallel rotating disks besides applications to turbomachinery can also be regarded as a class of fundamental flows. This assertion becomes self-evident as the aspect ratio 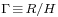 , (where
, (where 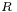 is the disk radius and
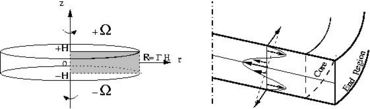
is the disk radius and 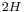 is the inter-disk spacing) is very large. In such case, self-similar solutions valid for disks with infinite radius are a good approximation of the exact solutions of the realistic closed geometry (i.e. finite radius). The self-similar solution is valid in the core region (see figure 1) but restrictions apply in the end-region or when the Reynolds number is above a threshold for which the flow is prone to instability. The Reynolds number is here defined by
is the inter-disk spacing) is very large. In such case, self-similar solutions valid for disks with infinite radius are a good approximation of the exact solutions of the realistic closed geometry (i.e. finite radius). The self-similar solution is valid in the core region (see figure 1) but restrictions apply in the end-region or when the Reynolds number is above a threshold for which the flow is prone to instability. The Reynolds number is here defined by 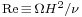 ,
, 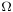 being the magnitude of the angular velocity and
being the magnitude of the angular velocity and 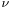 the kinematic viscosity. In two different studies [1] and [2], we focus our efforts on the particular case of exactly counter-rotating disks and address the question of the stability of such flows.
the kinematic viscosity. In two different studies [1] and [2], we focus our efforts on the particular case of exactly counter-rotating disks and address the question of the stability of such flows.
Results
Axisymmetric and asymptotic analysis
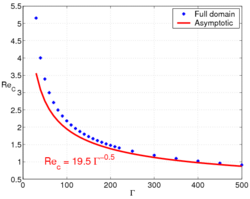
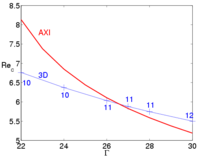
In a first study [1], we restricted ourselves to axisymmetric perturbations. In figure 2, the critical Reynolds number for the first bifurcation is plotted as a function of the aspect ratio. It is tempting but erroneous to think that the instability is a shear flow like instability. In such case, as the amplitude of the perturbation is large close to the end region (see figure 3), one would pick a scaling with 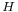 for length and
for length and 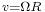 for velocity, where
for velocity, where 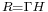 stands for the dimensional radius; the critical Reynolds number as defined in the previous section would have scaled as
stands for the dimensional radius; the critical Reynolds number as defined in the previous section would have scaled as 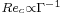 . Obviously, this does not fit with the full domain numerical results in figure 2 for which a scaling law is
. Obviously, this does not fit with the full domain numerical results in figure 2 for which a scaling law is 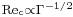 . Another explanation has to be found.
. Another explanation has to be found.
| Axisymmetric full domain computation | Local asymptotic parallel flow approximation |
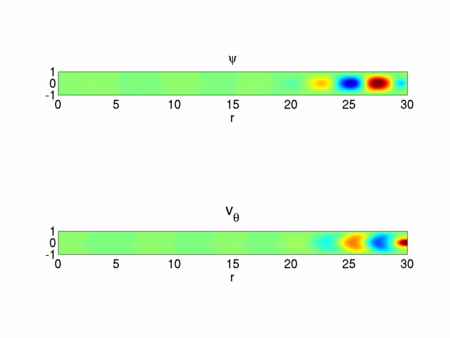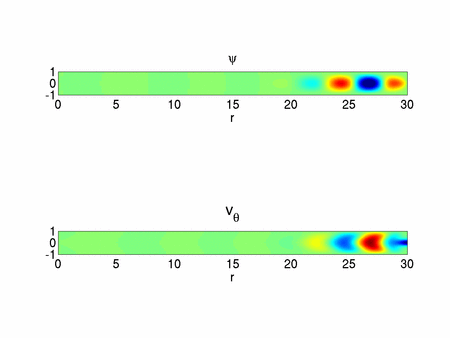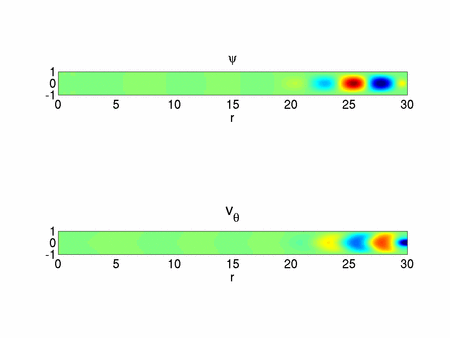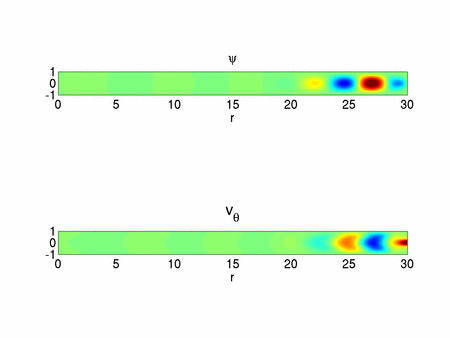
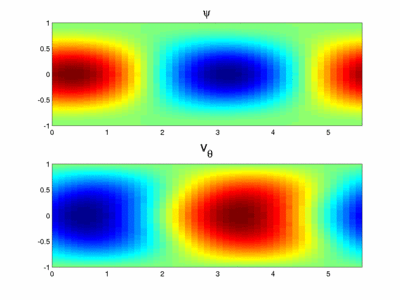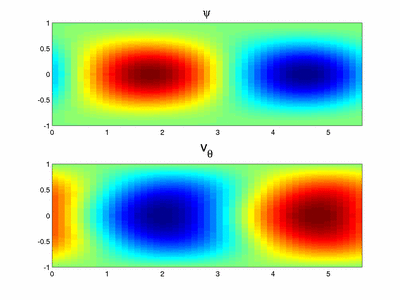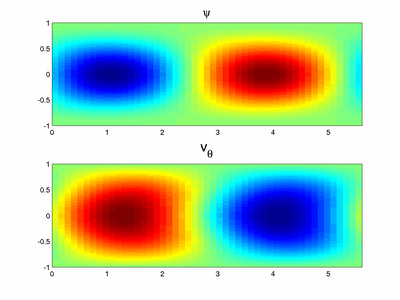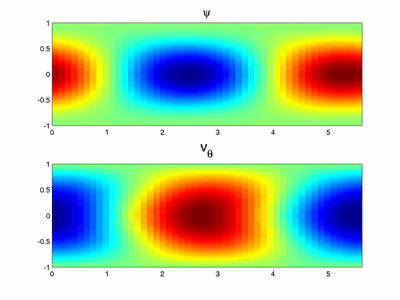
In the asymptotic analysis for large 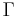 , the appropriate scalings lead to the Navier-Stokes equations in a Cartesian frame (i.e. all curvature terms vanish) with an additional centrifugal acceleration. In the core region and to leading order, the base flow is a parallel flow. This allows us to use a Fourier decomposition along the radial direction (see figure 4). The results of the linear stability analysis of this parallel flow are in good agreement with the full domain simulations not only qualitatively (see figure 3 and 4) but also quantitatively (see figure 2) which proves that the key ingredient of the instability is well captured in this simple model. The
, the appropriate scalings lead to the Navier-Stokes equations in a Cartesian frame (i.e. all curvature terms vanish) with an additional centrifugal acceleration. In the core region and to leading order, the base flow is a parallel flow. This allows us to use a Fourier decomposition along the radial direction (see figure 4). The results of the linear stability analysis of this parallel flow are in good agreement with the full domain simulations not only qualitatively (see figure 3 and 4) but also quantitatively (see figure 2) which proves that the key ingredient of the instability is well captured in this simple model. The 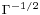 scaling and the centrifugal nature of the instability is now understood thanks to this asymptotic analysis. The physical mechanism invoking the coupling between the azimuthal velocity and the centrifugal acceleration is explained in [1].
scaling and the centrifugal nature of the instability is now understood thanks to this asymptotic analysis. The physical mechanism invoking the coupling between the azimuthal velocity and the centrifugal acceleration is explained in [1].
Three-dimensional, fully nonlinear and experimental results
In a second study [2], the bifurcations and the nonlinear dynamics are numerically and experimentally investigated. A linear stability analysis performed for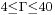 shows that nonaxisymmetric and axisymmetric modes can be stationary or time dependent in this range. Three-dimensional modes are dominant for
shows that nonaxisymmetric and axisymmetric modes can be stationary or time dependent in this range. Three-dimensional modes are dominant for 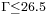 while axisymmetric modes are critical for
while axisymmetric modes are critical for 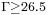 (see figure 5). The restriction to axisymmetry in the study [1] finds herein some justifications. In the particular case of
(see figure 5). The restriction to axisymmetry in the study [1] finds herein some justifications. In the particular case of 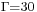 , nonlinear computations are performed at Reynolds numbers slightly above threshold and are compared to experimental results, showing the competition between axisymmetric and three-dimensional modes. For such aspect ratio, the linear stability analysis predicts
, nonlinear computations are performed at Reynolds numbers slightly above threshold and are compared to experimental results, showing the competition between axisymmetric and three-dimensional modes. For such aspect ratio, the linear stability analysis predicts 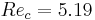 for
for 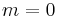 and
and 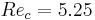 for
for 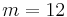 . For
. For 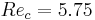 ,
, 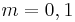 and
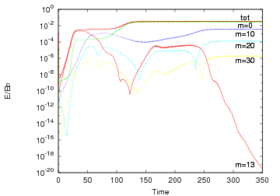
and 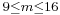 are all unstable. In figure 6, time evolution of dominant modal energies shows that
are all unstable. In figure 6, time evolution of dominant modal energies shows that 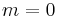 becomes dominant at
becomes dominant at 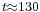 and, for three-dimensional modes, only
and, for three-dimensional modes, only 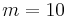 and its harmonics (not represented) remain and contain
and its harmonics (not represented) remain and contain 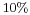 of the total fluctuating energy. This result could not be predicted by the linear stability analysis as growth rates for
of the total fluctuating energy. This result could not be predicted by the linear stability analysis as growth rates for 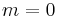 and
and  are smaller than the one for
are smaller than the one for 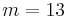 .
.
Conclusions and further work
Different tools have been used to study the stability of the flow between two exactly counter-rotating disks. An asymptotic analysis allowed us to find the mechanism of the dominant axisymmetric instability for large aspect ratio which takes place in the core region and gets stronger as it moves toward the periphery. The linear analysis showed that three-dimensional modes exist and nonlinear computations revealed that their amplitude stays relatively weak with patterns confined very close to the periphery of the disks as shown in figure 7. All these results and observations are in qualitative agreement with an experiment performed in Laboratoire d’Etudes Aérodynamiques de Poitiers (see figure 8). The three-dimensional mode selection in the nonlinear regime is still an open question. The case where the z-symmetry is lost, e.g. imposing different angular rotation rate of the disks, will be an interesting extension of the present work.
References
- [1] Martin Witkowski L, Delbende I, Le Quéré P, Walker J.S: Axisymmetric stability of the flow between two exactly counter-rotating disks with large aspect ratio, J. Fluid Mech, vol 546, p. 193-202, 2006.
- [2] Nore C, Martin Witkowski L, Foucault E, Pécheux J, Daube O, Le Quéré P: Competition between axisymmetric and three-dimensional patterns between exactly counter-rotating disks, Phys. Fluids, 054102 (12 pages), vol 18, 2006.
 .
.
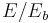 normalized by the basic state energy at
normalized by the basic state energy at 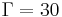 and
and 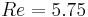 . The
. The 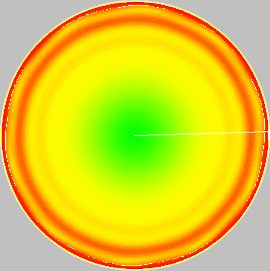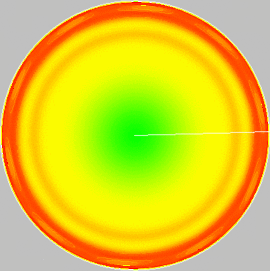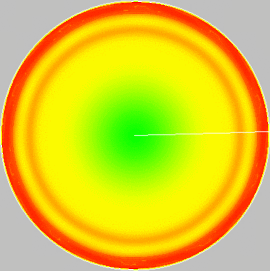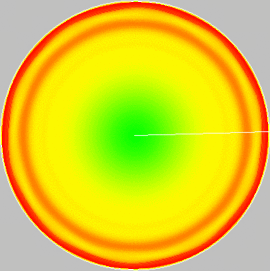

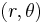 plane. Only part of the domain is seen on the picture.
plane. Only part of the domain is seen on the picture.