Stability study of the floating zone with respect to the Prandtl number value
Claudine Delcarte in collaboration with Othman Bouizi(CEA) and Guillaume Kasperski(FAST)
Contents |
Object
Thermocapillary convection in a laterally
heated liquid bridge is studied numerically, using a Chebyshev
spectral method. The stability of the axisymmetric basic state, with
respect to 3D perturbations, is characterized over a large range of
Prandtl number values (![Pr \in [10^{-3},10^2]](../upload/math/0/f/d/0fd4d7eeff9a2fbdd236b1fca73a87f9.png) ). First 3D non-linear spectral
computations are presented.
). First 3D non-linear spectral
computations are presented.
The industrial problem
Hydrodynamics in a laterally heated liquid bridge is studied in a zero gravity environment. This configuration is related to the floating zone crystal growth technique, that consists in translating a feed rod through a heating coil: the material progressively melts and solidifies on a seed as a single crystal. Experiments have shown detrimental striations in the chemical composition of some crystals. They are due to oscillatory thermocapillary flows. It is thus interesting to study the mechanisms responsible for the instability of the steady flows with a view to obtain higher quality products.
The mathematical model and the numerical methods
A simplified model of liquid bridge is adopted. The liquid is maintained by capillarity between two parallel concentric, solid and isothermal disks; they are kept at the uniform melting temperature. Neglecting static and dynamic deformations, the free surface is assumed to be cylindrical. It is submitted to a steady heating flux.
The thermocapillary convective flow is governed by the Navier-Stokes and energy equations associated to boundary conditions which include the source of the flow. The mathematical system is solved with a spectral collocation code. A continuation method based on a Newton algorithm allows to accurately follow the basic states with respect to the Marangoni and Prandtl values. Due to the geometry of the liquid bridge and the symmetry of the boundary conditions, the basic state is a 2D steady flow mainly constituted by two toroidal cells which are mirror symmetric with respect to the equatorial plane. The stability of the flows is investigated by an Arnoldi solver.
Results
These results are published in the referenced paper.
Linear stability analysis
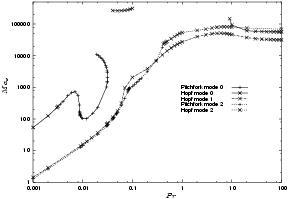
Figure 1 indicates the
bifurcation types and critical Marangoni values of the modes k=0,
1, 2 as a function of the Prandtl number value. For
all studied Pr values, we observe a transition of the axisymmetric
steady flow to a three-dimensional
flow. At low Prandtl number values, Pr < 0.3, the first destabilizing eigenmode is real and corresponds to a
wave number 2; it is directly followed by an oscillatory disturbance
with wave number 1. While for Pr > 0.3, the two first
disturbances are oscillatory modes with wave number 1 and 2 or 0
respectively. The behaviour of the Ma_c thresholds and frequencies in case of
Hopf bifurcations are quite different at low and high Pr number
values. The constant value of the critical Reynolds number Re_c=
Ma_c/Pr, at low Pr, indicates hydrodynamic perturbations while
at, Pr>1, the rather constant Ma_c value is the signature of
hydrothermal perturbations.
For large ranges of Prandtl values, the first destabilizing eigenmode breaks the symmetry around the equatorial plane. It is the case of the mode k=2 for
![Pr\in[0.001,0.047]](../upload/math/f/5/8/f588cc76019c31eb48af88b4e08dfe27.png) , and
, and ![Pr\in[0.085,0.4]](../upload/math/1/a/5/1a51a83368a46f557f504cd2f09e7797.png) . Figure 2 shows the structure of the oscillatory mode k=1 at Pr= 20 : the mirror symmetry is broken.
. Figure 2 shows the structure of the oscillatory mode k=1 at Pr= 20 : the mirror symmetry is broken.
3D flows
Low Prandtl number values
The important point, particularly for the experimenter, is to know what will be the non-linear flow behaviour at a Marangoni value just above the two thresholds.
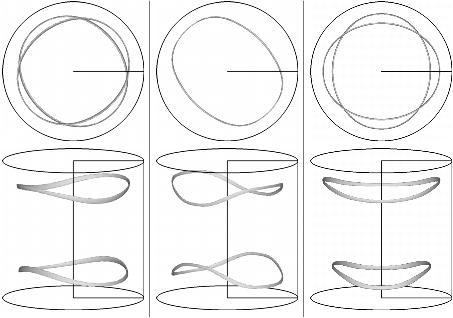
Figure 3 exhibits the flow loci where the velocity is zero at Pr=0.01, Pr=0.06 and Pr=0.2 respectively, at a time equal to 1500 thermal time units. All the odd
modes have canceled. The mode k=2 prevails in the instability
behaviour. In the regions where this mode is not symmetric with
respect to the equatorial plane (left and right panels), there is a
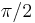 shift between the upper and lower curves related to the
azimuthal component of the mode 2 while its axial velocity has moved
the tori hearts is the same axial direction. This shift does not
exist in the center panel where the tori hearts are moved in
opposite directions. This is in complete agreement with the symmetry
properties of the components of the destabilizing modes.
shift between the upper and lower curves related to the
azimuthal component of the mode 2 while its axial velocity has moved
the tori hearts is the same axial direction. This shift does not
exist in the center panel where the tori hearts are moved in
opposite directions. This is in complete agreement with the symmetry
properties of the components of the destabilizing modes.
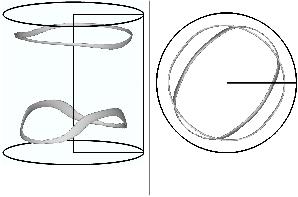
The flows at Pr=0.06 and Pr=0.2 are stable past 1500 thermal time units. Such is not the case for Pr=0.01. The resulting flow is unstable via a mode 1, different from the one obtained with the linear stability analysis of the basic flow: it is now a steady mode. Thus, the non-linear 3D flow at low-Pr does not always keep the properties nor structure of the initial critical modes. The resulting saturated 3D flow is neither symmetric nor anti-symmetric with respect to the mid-plane, as shown in Figure 4.
High Prandtl number values
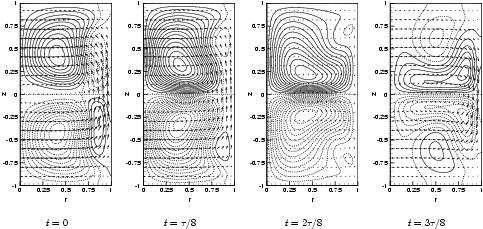
At Pr=100, the axisymmetric flow bifurcates via a Hopf bifurcation at Ma_c = 31647. We have calculated the 3D flow at Ma=35000, 40000 and 50000 over more than 20 thermal times, namely 2000 viscous times. We observed a steading wave.
Figure 5 depicts, in an axial
cut, at 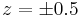 , and on a half-period, the temperature isolines
and velocity vectors of the disturbance (upper panel) and of the 3D
flow without the axisymmetric contribution (lower panel). The flow
is clearly governed by the destabilizing mode dynamics. Bringing Figures 2 and 5 together, shows that the
region of the steady state near
, and on a half-period, the temperature isolines
and velocity vectors of the disturbance (upper panel) and of the 3D
flow without the axisymmetric contribution (lower panel). The flow
is clearly governed by the destabilizing mode dynamics. Bringing Figures 2 and 5 together, shows that the
region of the steady state near 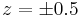 are shifted in opposite
radial directions in a plane along
are shifted in opposite
radial directions in a plane along 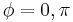 , while, at the same time, the fluid is
successively pushed up and down near the free surface.
, while, at the same time, the fluid is
successively pushed up and down near the free surface.
References
C. Bouizi, C. Delcarte and G. Kasperski, Stability study of the floating zone with respect to the Prandtl number value, Physics of Fluids, vol. 19, N°11, 2007.
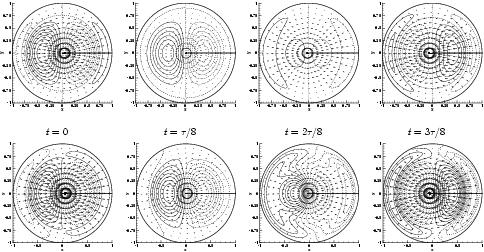
 of the perturbation (upper panel) and of the 3D flow without the 2D contribution (lower panel) at Ma=35000.
of the perturbation (upper panel) and of the 3D flow without the 2D contribution (lower panel) at Ma=35000.