Detection of Glottal Closing Instant on Electroglottographic Signal by a Threshold Method and on Acoustic Signal by Wavelets Transform
Vu Ngoc Tuan, C. d’Alessandro
Contents |
Introduction
In the production of voice, the vocal folds produces a excitation signal to the vocal tract. The vocal folds opens and closes by the effect of the air-flow coming from the lungs. A closing of the glottal induces a acoustic signal with a great amplitude. So after each glottal closing instant (GCI), the acoustic signal has a local maximum, the instant of this occurence is called LMI.
The aim of this article is to examine the correlation between GCI and LMI.
The method developped is as following : first, detection of
the GCI on the derivative of an electroglottographic signal (DEGG),
second, detection of LMI by a Wavelets Transform. These two detection
methods are perfomed on a corpus of vietnameses syllables. The inverse
of the duration between two GCI (or two LMI) is defined as a
GCI-fundamental frequency ,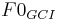 , or respectively LMI-fundamental
frequency
, or respectively LMI-fundamental
frequency 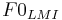 .
.
The correlation between GCI and LMI is examined by comparing these two fundamental frequencies.
GCI detection by electroglottography (EGG)
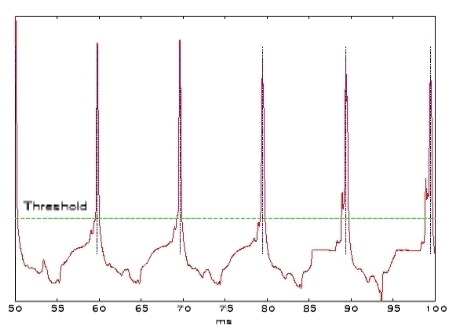
We use the derivative of th electroglottographic (DEGG) signal to detect the GCI, which is marked by a great positive peak. The detection of these peaks is done by a threshold method.[ref 1]. The duration between two peaks is the period of the acoustic signal and the F0 is calculated as the inverse of this period.
LMI detection by Wavelets Transform (WT) of the acoustic signal
A bank filter (6 filters) is applied to the acoustic signal (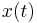 )
to calculate the WT of this signal. The transfert function (
)
to calculate the WT of this signal. The transfert function (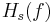 )
of these filters are defined by :
)
of these filters are defined by :
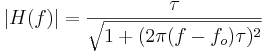
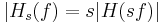
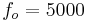 Hz ;
Hz ; 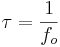 et s=1,2,4,8,16 et 32.
et s=1,2,4,8,16 et 32.
The output signal of the filters (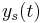 ) are calcultated as following :
) are calcultated as following :
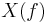 = Fourier Transform of
= Fourier Transform of 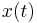
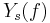 = Fourier Transform of
= Fourier Transform of 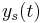
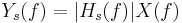
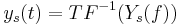
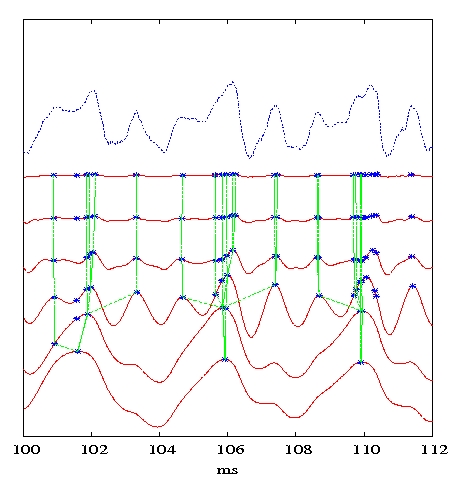
An example of the result of such calculation is shown is the next figure :
The signal at the top is 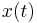 and the others are
and the others are 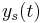 from top
(
from top
(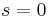 ) to bottom (
) to bottom (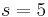 )
)
The maxima of 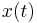 are reproduced in the
are reproduced in the 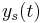 , these maxima are
followed by dynamic programming, which defines lines of maxima. The
summations of the amplitude along each line are proceeded. GCI are the
instant where the lines, with the greatest summation, point at the
output of the filter with s=0 .
, these maxima are
followed by dynamic programming, which defines lines of maxima. The
summations of the amplitude along each line are proceeded. GCI are the
instant where the lines, with the greatest summation, point at the
output of the filter with s=0 .
Relation between GCI and LMI
After each GCI there is a LMI, to point out the correlation between these
two events, two F0 are calculated :  deduced from
the GCI and
deduced from
the GCI and 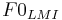 from LMI. These calculations are
done on the signal of a vietnamese syllables, consisted of a consonant
followed by the vowel /a/, with 21 consonants and six tones for each
syllable. The effect of tone is to modulate F0. The syllables are
realised by 6 speakers, three females and three males.
from LMI. These calculations are
done on the signal of a vietnamese syllables, consisted of a consonant
followed by the vowel /a/, with 21 consonants and six tones for each
syllable. The effect of tone is to modulate F0. The syllables are
realised by 6 speakers, three females and three males.
For each speaker and each tone 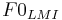 and the differences
and the differences
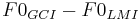 are calculated. Statistical average values are
calculated by taking into account the 21 consonants :
are calculated. Statistical average values are
calculated by taking into account the 21 consonants :
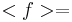 average of
average of 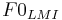 ;
; 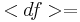 average of
average of 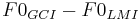 ;
;
relative error 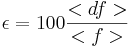 ; standard deviation
; standard deviation 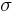
and the ratio 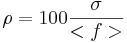
The results show that in most of the case,  is less than 5
% and
is less than 5
% and 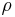 less than 10 %. So in the time intervlas, where such
results are obtained, LMI and GCI are correlated. In these time
intervals, the acoustic signal is stationnary, i.d the voice quality
is well defined (breath, whisper or voiced phonation). Between two
stationnary intervals, the acoustic signal evolves and there are
several maxima whose amplitude are nearly equal in the same period, in
this case the LMI detection fails.
less than 10 %. So in the time intervlas, where such
results are obtained, LMI and GCI are correlated. In these time
intervals, the acoustic signal is stationnary, i.d the voice quality
is well defined (breath, whisper or voiced phonation). Between two
stationnary intervals, the acoustic signal evolves and there are
several maxima whose amplitude are nearly equal in the same period, in
this case the LMI detection fails.
Conclusion
This article presents a method for detecting the glottal closing instant on the derivative of electroglottographic signal and an another method using Wavelets Transform for detecting the local maxima of the acoustic signal, which are induced by the closing of the glottal. The results show that these two events are correlated in the case of stable vowel, where the voice quality is well defined. Between two time intervals where the voice quality is well defined, the detection of the local maxima fails.
References
- Robust Glottal Closure Detection using the Wavelet Transform
Vu Ngoc Tuan & Christophe d'Alessandro
Proceedings of Eurospeech 99 Budapest
Budapest, Hungary (1999) vol.6 pages 2805-2808
- Glottal Closure Detection using EGG and the Wavelet Transform
Vu Ngoc Tuan & Christophe d'Alessandro
Advances in Quantitative Laryngoscopy, Voice and Speech Research
Proceedings of the 4th International Workshop
Jena, Germany (2000) pages 147-154
- Using Open Quotient for Characterisation of Vietnamese Glottalised Tones
Vu Ngoc Tuan, Christophe d'Alessandro, Alexis Michaud
Proceedings of Interspeech Lisbonne Lisbonne, Portugal (2005) pages 2885-2889