Comparative evaluation of the ZZT and inverse filtering for voice source analysis
N. Sturmel, C. d’Alessandro, B. Doval
A new method for voice source estimation is evaluated and compared to Linear Prediction (LP) inverse filtering methods (autocorrelation LPC, covariance LPC and IAIF [1] ). The method is based on a causal/anticausal model of the voice source and the ZZT (Zeros of Z-Transform) representation [2] for causal/anticausal signal separation. A database containing synthetic speech with various voice source settings and natural speech with acoustic and electro-glottographic signals was recorded. Formal evaluation of source estimation is based on spectral distances. The results show that the ZZT causal/anticausal decomposition method outperforms LP in voice source estimation both for synthetic and natural signals. However, its computational load is much heavier (despite a very simple principle) and the method seems sensitive to noise and computation precision errors.
Contents |
Introduction
The Zeros of the Z Transform (ZZT [2]) is a new speech decomposition method that denotes with traditional linear prediction (LP) based algorithms as it relies on a mixed phase model of speech production. This model will be first presented, then the algorithm used for the ZZT decomposition. Our goal here is to show a comparative study of the ZZT versus widely used LP methods, the protocol used and some of the results obtained are also shown here.
The comparision will first take place on synthetic signals (with 4 of the 5 glottal parameters varying), then on real speech sample.
Mixed phase speech production method
|
Voice source estimation is still a challenging problem for speech processing applications. Two broad classes of methods have been proposed so far : digital inverse filtering and source-tract deconvolution using the Fourier transform. On the one-hand, the Linear Predictive (LP) based methods take advantage of the autoregressive structure of the vocal tract acoustic filter. This filter structure is given by the linear acoustic model of speech production. LP can be extended to autoregressive and moving average (ARMA) inverse filter structures, but without clear improvement in source estimation. On the other hand Fourier Transform (FT) based methods take advantage of another feature of the speech production process, namely the multiplicative combination of source and filter in the frequency domain. For instance, homomorphic deconvolution methods (cepstrum) use the multiplication to addition transformation property of the logarithm for spectral envelope estimation. The Group Delay decomposition is another Fourier transform based deconvolution. Because of difficulties in phase unwrapping, these methods are scarcely used for voice source signal estimation. Recently, another feature of speech production process has been pointed out and a new deconvolution algorithm has been proposed for exploiting this feature [2,3]. The first keypoint of this new source estimation is the so-called Causal Anticausal Linear Model (CALM) of the voice source. It is shown in [3] that the glottal signal can be seen as an impulse train filtered by a causal/anticausal linear filter. Then the source-tract separation problem can be considered as a causal and anticausal filters identification problem. As for digital filters, causal (resp. anticausal) poles are placed inside (resp. outside) the unit circle, a simple criterion can be applied for sorting causal and anticausal contributions to the spectrum. The second key point of the separation algorithm is a method for causal and anticausal component estimation and separation : the so-called Zero of the Z transform (ZZT) signal representation [2]. In this method, a Z-transform polynomial is formed using the (windowed) signal samples of two speech periods. Precise centering of the analysis frame on the Glottal Closing Instant (GCI) is of paramount importance. The roots of this polynomial are the zeros of the Z-transform. It can be shown that roots outside (resp. inside) the unit circle correspond to the anticausal part of the voice source (resp. the causal part of source and vocal tract). A simple algorithm for source/filter separation has been proposed in [2]. This new method gave very promising results. However, to go a step further, a formal comparative evaluation of the method is needed. The aim of the present work is a formal evaluation of the performances on voice source estimation for this new method, and a comparison with the results of three main inverse filtering method currently used in speech processing applications. |
|
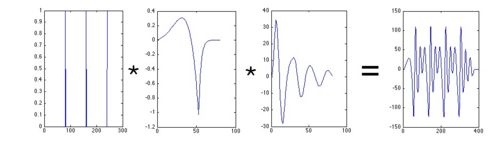
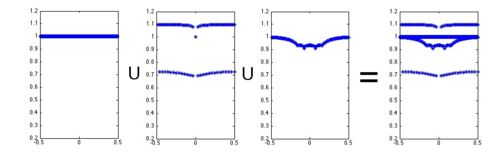
The first three figure are the illustration of the so called Causal/Anti-causal model. From left to right : Periodic component, Source component, Vocal tract filter, full voice signal. From top to bottom, for each component of the signal : time signals, spectrums, ZZT representation. Last figure is the list of the parameters used for glottal wave synthesis and their definition according to LF parameters. Most important parameters are |
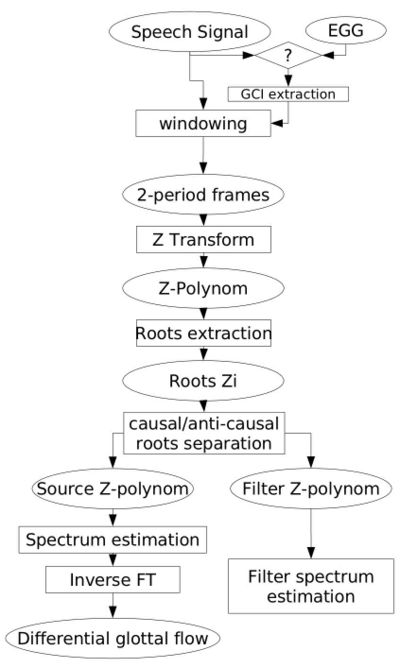
The ZZT decomposition algorithm
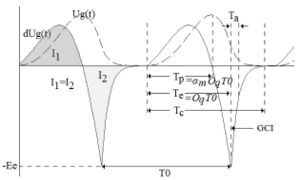
ZZT algorithm relies on exact positionning on the analysis window. In order to achieve maximum phase coherence, the center of the anaylsis window (chosen to have the best size at two times the pitch period) has to be on a glottal closing instant (GCI). Those instant can be estimated by various method, and we chose here to record simultaneous EGG signals on real speech, in order to extract GCI and open quotient 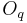 .
.
- First, GCI points need to be detected, either by synchronous electro-glottographic (EGG) recording analysis or by direct extraction from the speech signal itself.
- The signal is truncated in two periods frames, using GCI informations.
- Each frame is windowed using a blackman window.
- Roots
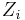 of the associated polynomial
of the associated polynomial 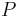 (the frame Z-transform) are computed :
(the frame Z-transform) are computed :
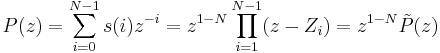
- The zeros are sorted for separation of the anticausal (G) and causal (F) components of the signal, note that
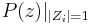 corresponds to a periodic component, unlikely to happen in non harmonic spectrum signals :
corresponds to a periodic component, unlikely to happen in non harmonic spectrum signals :
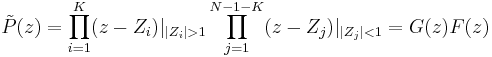
- Causal and Anticausal spectra are computed
- Glottal flow waveform can therefore be obtained by inverse FT.
Linear Prediction Methods
| Method | Auto-correlation | Burg | Covariance | IAIF [1] |
| Computation | center on the whole speech sample | 20ms speech segment | performed only on closed phase | 20ms speech segment |
| Order | always 18 | 18 | maximum 18 | always 18 |
| pre-emphasis | high pass filter 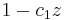 with with 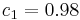 } } |
high pass filter 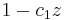 with with 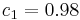 } } |
high pass filter 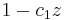 with with 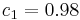 } } |
adjusted by the algorithm (first order filter) |
The inverse filtering uses LP estimation of the vocal tract filter. Each of the four algorithm presented has its own pros and cons, and was chosen for its simplicity and/or its widespeard use. When the vocal tract filter transfer function A is estimated (A being the autoregressive filter coefficient), glottal flow is obtained by filtering :
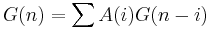
Synthetic test signals
Synthetic test signals are generated using the LF model [7] rewritten as in [8] and a formant synthesizer with three implemented filters : a synthetic /a/ and /i/ computed according to common formant frequencies and bandwidths and two natural filters obtained by lpc analysis : real /i/ and real /u/.
Open quotient (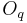 ), Fundamental period (
), Fundamental period (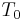 ) and Asymmetry (
) and Asymmetry (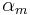 [8], corresponding to
[8], corresponding to 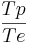 parameter in the LF model) are varying among test condition. The remaining parameter, the return phase quotient, is set to zero as
it belongs to the causal part of the differential glottal flow and can therefore
not be estimated by ZZT. Preliminary tests showed that the effect of the return phase quotient on lp-based source estimation is negligible. This parameter is then not considered in this study.
parameter in the LF model) are varying among test condition. The remaining parameter, the return phase quotient, is set to zero as
it belongs to the causal part of the differential glottal flow and can therefore
not be estimated by ZZT. Preliminary tests showed that the effect of the return phase quotient on lp-based source estimation is negligible. This parameter is then not considered in this study.
The test is performed with the following parameter variations:
-
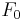 (90, 110, 150, 190, 230, 270, 330 Hz)
(90, 110, 150, 190, 230, 270, 330 Hz)
-
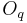 from 0.3 to 0.9 by 0.05 steps (13 values)
from 0.3 to 0.9 by 0.05 steps (13 values)
-
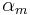 from 0.6 to 0.85 by 0.05 steps (6 values)
from 0.6 to 0.85 by 0.05 steps (6 values)
- Vowels among the three chosen (/a/, /i/, real /i/, real /u/)
- Noise/Signal ratio : -300dB (noiseless signal), -60dB (ambiant recording white noise simulation)
Measure Method
The evaluation criterion is based on spectral distance between estimates and synthetised glottal flows. When trying to estimate other source parameters than the open quotient, fine estimation of the source spectrum has a proeminent role. This is why this criterion was chosen, because spectral distance does not only measure adequacy in formant frequency and bandwith estimation, but also on spectral tilt restitution on the source spectrum. The error 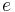 , is computed on a restrained range of frequency :
, is computed on a restrained range of frequency :
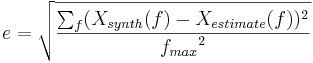
The frequency range was chosen to be from 0 to 4000 Hz to evaluate the low frequency accuracy of the estimation, that is mainly linked to the value of 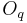 . Also, since GCI is imposed by the ZZT estimation method, it's high frequency accuracy is substantialy better and a wider frequency range would have disadvantaged LP estimation.
. Also, since GCI is imposed by the ZZT estimation method, it's high frequency accuracy is substantialy better and a wider frequency range would have disadvantaged LP estimation.
Synthetic signals results
| vowel /a/ | vowel /i/ | vowel real /i/ | vowel real /u/ | ||||||||||||||||||
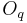 |
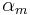 |
Autoc. | Cov. | Burg | ZZT | IAIF | Autoc. | Cov. | Burg | ZZT | IAIF | Autoc. | Cov. | Burg | ZZT | IAIF | Autoc. | Cov. | Burg | ZZT | IAIF |
| 0.3 | 0.65 | 3.43 | 9.87 | 3.44 | 0.87 | 2.86 | 3.32 | 9.21 | 3.27 | 1.56 | 2.98 | 4.4 | 6.2 | 3.83 | 1.62 | 3.33 | 3.98 | 5.97 | 3.95 | 1.61 | 4.26 |
| 0.3 | 0.8 | 3.27 | 10.39 | 3.37 | 0.73 | 2.5 | 3.38 | 8.41 | 3.41 | 1.57 | 3.13 | 4.7 | 6.99 | 4.73 | 1 | 2.22 | 4.45 | 6.28 | 4.5 | 1.63 | 3.98 |
| 0.5 | 0.65 | 2.79 | 9.4 | 2.65 | 0.79 | 3.21 | 2.71 | 8.91 | 2.47 | 1.66 | 2.82 | 3.37 | 7.43 | 3.3 | 1.07 | 3.12 | 3.55 | 6.11 | 3.35 | 2.12 | 4.42 |
| 0.5 | 0.8 | 2.22 | 9.01 | 2.27 | 0.73 | 2.41 | 2.48 | 8.66 | 2.49 | 1.37 | 2.82 | 2.9 | 6.87 | 3 | 1.19 | 1.69 | 2.9 | 6.44 | 2.96 | 1.51 | 2.47 |
| 0.7 | 0.65 | 2.9 | 11.71 | 2.56 | 1.81 | 3.32 | 2.82 | 10.08 | 2.49 | 2.09 | 2.62 | 4.2 | 6.64 | 3.88 | 1.39 | 4.32 | 4.02 | 7.5 | 3.68 | 2.76 | 5.17 |
| 0.7 | 0.8 | 1.73 | 11.49 | 1.84 | 0.69 | 2.51 | 1.99 | 9.74 | 2.05 | 1.4 | 3.17 | 1.74 | 7.59 | 1.85 | 1.03 | 1.78 | 2.23 | 7.29 | 2.28 | 1.59 | 1.93 |
| vowel /a/ | vowel /i/ | vowel real /i/ | vowel real /u/ | |||||||||||||||||
| F0 | Autoc. | Cov. | Burg | ZZT | IAIF | Autoc. | Cov. | Burg | ZZT | IAIF | Autoc. | Cov. | Burg | ZZT | IAIF | Autoc. | Cov. | Burg | ZZT | IAIF |
| 90 | 2.17 | 5.59 | 2.15 | 0.22 | 2.22 | 2.22 | 5.3 | 2.21 | 0.87 | 2.51 | 2.44 | 6.54 | 2.38 | 0.43 | 2.09 | 2.76 | 5.07 | 2.68 | 0.35 | 2.9 |
| 110 | 2.21 | 5.62 | 2.2 | 0.37 | 2.53 | 2.29 | 5.49 | 2.28 | 1.23 | 2.53 | 2.48 | 6.78 | 2.42 | 0.61 | 2.05 | 2.87 | 5.93 | 2.81 | 1.5 | 2.97 |
| 150 | 2.31 | 8.24 | 2.3 | 0.33 | 2.79 | 2.55 | 7.86 | 2.54 | 1.51 | 3.16 | 2.89 | 6.84 | 2.84 | 0.95 | 2.26 | 2.81 | 8.01 | 2.78 | 0.73 | 2.92 |
| 190 | 2.43 | 14.12 | 2.42 | 0.42 | 2.96 | 2.46 | 13.72 | 2.41 | 1.66 | 2.74 | 3.16 | 8.38 | 3.14 | 1.47 | 2.59 | 3.11 | 6.67 | 3.12 | 0.97 | 3 |
| 230 | 2.7 | 9.58 | 2.71 | 1.18 | 3.43 | 3.24 | 7.43 | 3.22 | 2.97 | 3.46 | 3.55 | 6.35 | 3.6 | 1.87 | 3.1 | 3.89 | 5.62 | 3.81 | 2.59 | 3.89 |
| 290 | 3.12 | 15.73 | 3.15 | 2.29 | 3.14 | 3.5 | 10.24 | 3.45 | 1.99 | 3.14 | 4.16 | 6.27 | 4.24 | 1.55 | 4.01 | 3.93 | 8.18 | 3.92 | 3.13 | 3.95 |
| 330 | 3.93 | 13.64 | 3.94 | 3.27 | 3.85 | 3.63 | 13.49 | 3.55 | 2.84 | 3.71 | 4.56 | 5.91 | 4.65 | 1.95 | 4.39 | 5.01 | 7.2 | 4.99 | 4.22 | 5.3 |
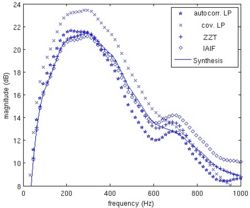
Direct results of the benchmark are the cumulative spectral distances presented on table above. Lowest values (highlighted in dark yellow) represent the closest spectrum to the original used for synthesis ; note that in every condition ZZT gives the best result by far, and that IAIF and autocorrelation LP show both good performances too.
Spectral distance results are leading to the following observations:
- The pitch synchronous covariance linear prediction seems the worst differential glottal wave
estimator. Since it is performed on a very short signal segment, the autoregressive filter order may probably be too small for accurate estimation of the vocal tract filter. Nevertheless, the overall low frequency restitution of the glottal formant is realist.
- The IAIF methods seems the most robust one tested in this paper in the sens that it gives good results in almost every case : the adaptive part of the algorithm appears
to be useful for fitting even the worst signals. However noise and ripples on the estimated differential glottal waveform make it hardly usable for parameter extraction or analysis.
- The auto-correlation linear prediction is sometimes the best LP-based source
estimation in this benchmark. However, tests on signals are using long analysis window, exploiting the time invariance assumed by the method. This is not always realistic for actual time-varying real speech signals. Furthermore, it can be seen on the table that the worst cases are those
were the pre-emphasis does not completely suppress the glottal formant :
low 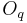 values leading to a glottal formant at two or three
times
values leading to a glottal formant at two or three
times 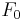 , and low values for
, and low values for 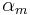 leading to a more resonant formant.
leading to a more resonant formant.
- The ZZT inverse filtering outperforms lp-based methods both in spectral measurements and time-domain observations. The absence of ripples in the glottal closed phase together with the very good benchmark results are the strongest arguments in favor of this method. However, the method relies heavily on precise glottal closing instants determination, and it seems also relatively weak for low signal to noise ratio. Computational load is heavier than for LP based methods, because it is based on roots extraction from a high degree polynomial.
Application to real speech
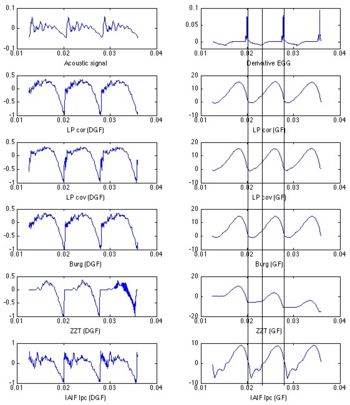
Source estimation examples are presented in the right side figure. It presents source estimations for a real speech signal. Both glottal flow and its derivative are shown for each method. An Electroglottographic reference is available for this example, showing that the open quotient is about 0.5 (i.e. the closed phase of the source is about half of the period).
In this example, the ZZT is the only method giving a closed phase of about 0.5. And therefore the only method meeting the asumption that there is no acoustic flow during the closed phase. The slight slope of the ZZT estimated glottal flow is an artefact of the spectral reconstruction. This example also shows that ZZT could be used for direct parameter estimation, such as 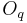 or even
or even 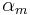 .
.
Conclusion
In this paper a new deconvolution method has been evaluated, based on an all zero estimation of the speech causal/anticausal linear model. It was compared with linear prediction based inverse filtering. The results showed that ZZT is a promising deconvolution method, able to outperform LP inverse filtering in every speech condition. Moreover the ZZT seems to be powerful for estimation of the glottal flow and its parameters, such as Oq. The main drawbacks are the computational cost, lack of robustness for noise corrupted signals and the paramount importance of accurate glottal closing instant detection.
References
[1] P. Alku, “Glottal wave analysis with pitch synchronous iterative adaptive inverse filtering”, Speech Communication, vol. 11, pp. 109–118, 1992.
[2] B. Bozkurt, B. Doval, C. d’Alessandro, and T. Dutoit, “Zeros of z-transform representation with application to source-filter separation in speech”, IEEE, vol. 12, pp. 344–347, 2005.
[3] B. Doval, C. d’Alessandro, and N. Henrich, “The voice source as a causal/anticausal linear filter”, proc. VOQUAL’03, ISCA Workshop, Geneva, Aug. 2003.
[4] J. D. Markel and A. H. Gray Jr, Linear Prediction of Speech, Springer Verlag, Berlin, 1976.
[5] J. Makhoul, “Linear prediction: A tutorial review”, Proc. IEEE, vol. 63(5), pp. 561–580, 04 1975.
[6] Wong D., Markel J., and Gray A. Jr, “Least squares glottal inverse filtering from the acoustic speech waveform”, IEEE trans., vol. 35, pp. 350–355, 1979.
[7] G. Fant, J. Liljencrants., and Q. Lin, “A four parameter model of glottal flow”, STL-QPSR, vol. 4, pp. 1–13, 1985.
[8] B. Doval, C. d’Alessandro, and N. Henrich, “The spectrum of glottal flow models”, acta acustica united with acustica, vol. 92, pp. 1026–1046, 2006.
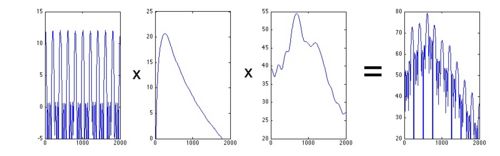
 was not studied here.
was not studied here.