Speech fundamental frequency estimation using the Alternate Comb
J.S.Liénard, F. Signol (PS), avec C.Barras (TLP)
Contents |
General framework
Artificial speech processing encounters severe difficulties when the signal to be processed is recorded in real life conditions, i.e. at some distance from the mouth of the speaker or in the presence of competing voices or other sounds. In contrast, the human is perfectly able to select and process the signal of interest in the acoustic environment. This capability is at the heart of Bregman's Auditory Scene Analysis [1]. We adopt the CASA (Computational ASA) point of view which, starting from ASA observations, aims at building systems able to overcome the present limitations. By now we are interested in the problem of separating two speech signals artificially mixed in a single acoustic channel, which constitutes a simplified form of the well-known Cocktail Party Effect [2]. In the present study we do not take into account the top-down aspects of the auditory processes (attention, behavioral considerations, use of the higher-level structures of speech) because we address the lowest level of auditory perception where, according to Bregman, structuration is essentially bottom-up.
Separating two mixed signals implies firstly the segregation of the mixture into elementary entities pertaining to one or the other signal and, secondly, their grouping into separate signals. Both operations should be based on discriminant features, to be extracted from the signal on a purely acoustical basis. The most important feature is the speech fundamental frequency F0, the perceptual aspect of which is named "pitch". However this feature is only defined in the "voiced" speech segments. Besides, it evolves from one instant to the next and it is often fuzzy or noisy, which renders its determination error-prone. In the traditional (monopitch) perspective it is implicitly hypothesized that the signal comprises only one voice. If one considers that several voices may be present in the signal (multipitch perspective), then it is extremely difficult to extract with certainty the voicing and pitch features necessary to the segregation-and-grouping process.
The pitch function
Let us consider a short speech signal segment (a few tens of ms) and an algorithm for computing its periodicity. The waveform is complex; its periodicity is not granted and often difficult to estimate. Thus the periodicity computation is repeated for a set of values Fc chosen in an arbitrary interval [Fcmin, Fcmax]. The result is a "pitch function", which tells how good is a given frequency Fc for representing the periodicity of the segment. The "goodness" of the measurement may be expressed in many forms: energy, magnitude, autocorrelation, decibels, plausibility, etc. Usually it is decided that the best estimate of F0 is the maximum of the pitch function, provided that it exceeds an arbitrary threshold. If the maximum lies under the threshold the segment is declared unvoiced.
However this procedure implies that there is only one periodicity in the signal, which cannot be asserted in the multipitch perspective. Besides, even in the monopitch case, the pitch function exhibits numerous local maxima, often of the same order of magnitude as the right one. Picking the wrong maximum produces what is called a "gross error". The usual practice is to consider that an estimate exceeding +- 20% (i.e. 3 semitones) of the right F0 is a gross error. The most frequent gross errors occur at the octave (Fc=2F0) and sub-octave (Fc=F0/2). The objective of the present study is to understand the origin of these gross errors in order to neutralize them.
Origin of the erroneous peaks of the pitch function
It has been known for a long time that trying to isolate the first harmonic (fundamental) of the speech spectrum in order to measure it was hopeless [3], mainly because the F0 interval of variation is large and a priori unknown. In some cases the fundamental is not even present (telephone transmission). Estimating F0 implies that several harmonics of the spectrum are taken into account in order to look for a common divisor, as evidenced by Schroeder [4]. One is always brought to compare a periodic structure to itself or to another one, by means of a recurrent delay or lag.
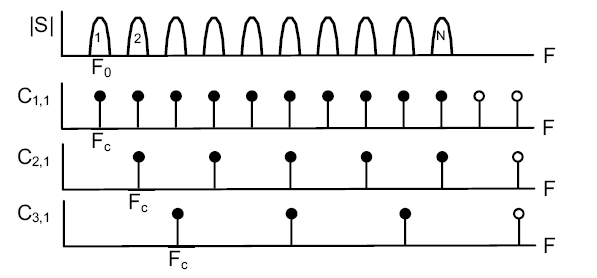
This mechanism is illustrated in figures 1 and 2 in the case of a schematic spectrum of fundamental frequency F0. The other periodic structure is a spectral comb, infinite and uniform, of fundamental frequency Fc.
The pitch function of figure 3 is computed as the scalar product of both, for frequencies Fc comprized in the interval [Fcmin, Fcmax]. The peaks of the pitch function indicate the values of Fc for which a maximum coincidence of both structures is obtained. They occur when the dilation factor Fc/F0 becomes equal to the irreducible ratio of two positive integers p/q. Integer p is the harmonic index, integer q is the sub-harmonic index. Any peak of the pitch function may be labeled with those two indices. The main peak labeled (1,1) corresponds to the correct estimation of F0.
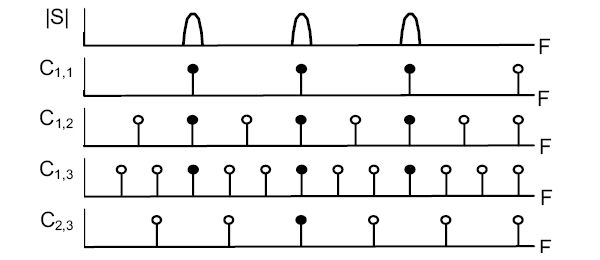
From the Simple Comb to the Alternate Comb
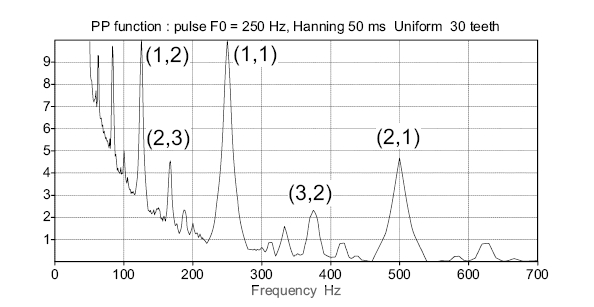
A pitch function such as the one represented on figure 3 cannot be used to estimate F0, because it exhibits several local maxima of high amplitude, in particular in the sub-harmonic region. These erroneous peaks can be attenuated by limiting the number of teeth of the comb, and by decreasing their magnitude as a function of their rank. This kind of comb first defined by [5] will be called here "Simple Comb". The pitch function obtained with it on the same sound as before shows the decrease of the sub harmonic peaks (figure 4). Consequently peak (1,1) is the global maximum and produces the correct estimate of F0.
However the modifications introduced in the Simple Comb affect the entire pitch function. Figure 4 shows that harmonic peaks such as (2,1) and (2,3) get reinforced in comparison to the main peak (1,1) and may yield some new gross errors. In order to reduce them we propose the Alternate Comb (figure 5), in which the main harmonic peaks are neutralized by means of negative teeth of adequate magnitude.
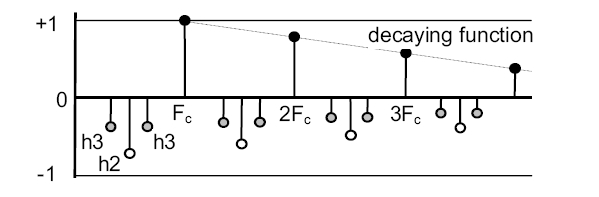
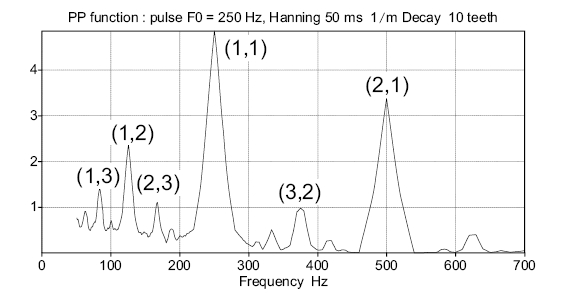
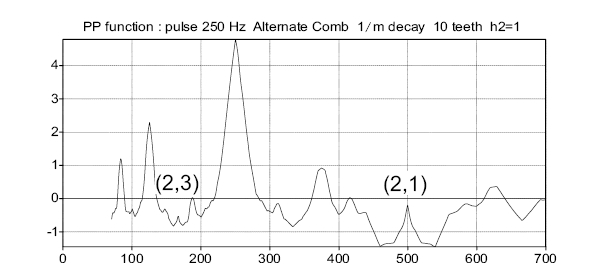
Figure 6 shows the effect of the single median negative tooth (octave cancellation: coefficient h2 set to 1, the others set to zero). Peaks (2,1) and (2,3) (and more generally all peaks (2,q)) get completely neutralized. This particular setting is practically equivalent to the SHR algorithm [6] which appears to obtain the best results published in the recent years. The Alternate Comb, based on a more general analysis, should perform similarly for the octave cancellation (h2=1), and better if negative teeth of higher order are taken into account.
Evaluation
In order to optimize and evaluate the Alternate Comb we used several classical databases specialized in pitch estimation. We conducted the optimization (mainly the h2 and h3 parameters) with the Keele database [7]. The best results were of the same order of magnitude, or better, than the ones given by other algorithms recognized as reprensenting the state of the art. Then, with the same parameter values, we used another database [8] to check the quality of the settings. In both cases the reference values were those given by the authors from the analysis of the electroglottographic signals recorded simultaneously from their speakers. The results are expressed in terms of voicing error rate (VUV) and gross error rate (GER).
| VUV % | GER % | |
|---|---|---|
| YIN (as reported in [9]) | n/a | 2.4 |
| SHRP (averaged from [6]) | n/a | 1.9 |
| Simple Comb h2=0 h3=0 | 13.5 | 3.2 |
| Alternate Comb h2=0.4 h3=0.2 | 12.3 | 1.8 |
| Alternate Comb h2=0.4 h3=0.2 width 80 ms | 14.9 | 1.1 |
| Praat: To Pitch... 0.01 75 600 (includes post-processing) | 10.6 | 1.6 |
Lines 1 and 2 of Table 1 reproduce the results published by [9] and [6] in test conditions as close as possible to ours (some differences subsist in the F0 range). The next 2 lines reflect the best results obtained with the Simple Comb (positive teeth only) and the Alternate Comb after optimization of the h2 and h3 coefficients. The 5th line was obtained with a time window of double duration (80 ms) which increased the frequential resolution and provided a better use of the negative teeth of the Alternate Comb in the case of very low voices.
The 6th line is somewhat different. It shows the results of the standard pitch algorithm available in the Praat software [10], which includes an extremely efficient post-processing taking into account the whole signal. This was not the case of the other algorithms reported, which were tested on a frame-by-frame basis. Thus a straightforward comparison with the results reported on the previous lines would not be fair. However the figures obtained reflect more or less an optimum of what could be extracted from the data in the monopitch perspective.
From these results it appears that the Alternate Comb performs extremely well on this database with results close to the optimum represented by a post-processed algorithm.
The results reported on table 2 were obtained from the Bagshaw database. They show that, here again, the frame-to-frame Alternate Comb performs practically as well as the Praat standard algorithm with its post-processing.
| F0 limits | VUV % | GER % | |
|---|---|---|---|
| Praat: To Pitch... 0.01 75 600 (includes post-processing) | 75-600 | 4.8 | 1.0 |
| Alternate Comb h2=0.4 h3=0.2 width=40 ms | 75-600 | 6.3 | 0.9 |
| Alternate Comb, voicing threshold x2 (discards most erroneous labels) | 75-600 | 12.0 | 0.3 |
The 3rd line reports the results of the Alternate Comb for which the value of the voicing threshold was doubled. The consequence of this was to decrease the number of frames considered as voiced. Thus the VUV criterion got poorer. But the GER criterion got much better, because the frames discarded were in majority the frames found at the beginning and ending of the voiced segments, where the labeling by the authors themselves was dubious. With this new setting the result of the Alternate Comb in terms of Gross Error Rate outperformed the best results previously published on this database.
Conclusion and perspectives
Our approach of pitch estimation by analysis and compensation of the secondary peaks of the pitch function is now validated in monopitch, on a frame-by-frame basis, by comparison with the state of the art, on classical databases. The study shows that the performance of any method is insufficiently specified by the gross error rate. The voicing error rate VUV must also be measured. For real speech material GER and VUV are interdependent. Also it appears quite clearly that both are strongly dependent on the choices made by the operator regarding the interval of F0 variation and the voicing threshold.
Actually voicing is an ambiguous notion. In phonology voicing is a binary concept (a phoneme is either voiced or unvoiced), including some knowledge of the langage structures at the phonetic and phonological levels. But its realization in the signal, considered on each single frame, is merely a certain degree of periodicity. Thus the transformation of the low-level degree of periodicity into the higher level state of the "Voiced" distinctive feature is a complex process, to study in the general framework of phonetic perception.
We are currently evaluating our approach in the multipitch situation, for which the evaluation methodologies are still in infancy [11]. We know for sure that the less parasitic peaks are prominent in the pitch function, the better any separation process will perform.
We also know that separation is a kind of chicken-and-egg problem: on one hand correct estimations of voicing and F0 contribute to the separation process; on the other hand, voicing and F0 features cannot be reliably extracted from the signal without some knowledge of the phonetic content of the signals to separate. Consequently we are interested in the processes by which series of instantaneous observations on the signal may be linked together to give birth to larger perceptual entities called "auditory streams" by Bregman. We consider the hypothesis according to which streaming, at the sub-phonetic perceptual level, cannot be entirely performed in a bottom-up manner but, instead, has to make use of some top-down flows of information.
References
1. Bregman A. S. Auditory scene analysis: the perceptual organization of sound, Cambridge, Mass., Bradford books (MIT Press), 1990.
2. Cherry C. "Some experiments on the recognition of speech, with one and with two ears", J. Acoust. Soc. Amer. 22, 5, 975-979, 1953.
3. Hess W. Pitch determination of speech signals, Springer Verlag, Berlin, 1983.
4. Schroeder M. R. "Period Histogram and Product Spectrum: New Methods for Fundamental-Frequency Measurement", J. Acoust. Soc. Amer., 43, 829-834, 1968.
5. Martin P. "Comparison of pitch detection by cepstrum and spectral comb analysis", IEEE ICASSP, 180-183, 1982.
6. Sun X. "Pitch determination and voice quality analysis using sub-harmonic-to-harmonic ratio", IEEE ICASSP, 333-336, Orlando, 2002.
7. Plante F., Ainsworth W.A. and Meyer G. "A Pitch Extraction Reference Database", Eurospeech, Madrid, 837-840, 1995.
8. Bagshaw P.C., Hiller S.M. and Jack M.A. "Enhanced pitch tracking and the processing of F0 contours for computer aided intonation teaching", Eurospeech, Berlin, 1993.
9. De Cheveigné A. "YIN, a fundamental frequency estimator for speech and music", J. Acoust. Soc. Amer., 111, 1917-1930, 2002.
10. Boersma P. "Accurate short-term analysis of the fundamental frequency and the harmonics-to-noise ratio of a sampled sound", Institute of Phonetic Sciences, University of Amsterdam, Proceedings 17, 97-110, 1993.
11. De Cheveigné A. "Multiple F0 estimation", in Computational Auditory Scene Analysis, Wang and Brown eds, IEEE Press, Wiley-Interscience, 2006.
Links
For a more detailed description of this work, see the communication to Interspeech 2007 : http://rs2007.limsi.fr/documents/PS_lienard.pdf