Some mathematical aspects of the Navier-Stokes equations

From 2007 Scientific Report

Jump to: navigation, search

J.L. Guermond in collaboration with "J. Shen" (Univ. of Purdue)

1 Object
2 Description
3 Results and prospect
4 references
5 Links

Object

This research program is twofold :

Analysizing fractional step methods for the Navier--Stokes equations. I have been working on this topic since 1993. Fractional step methods are time stepping algorithms for approximating the time-dependent incompressible Navier--Stokes equations. I collaborate on this problem with with Jie Shen (prof. Univ. of Purdue) since 2000. We have proved original convergence results.
Formalizing mathematically the so-called Large-Eddy Simulation methods (LES). I started this research program in 1997. The acronym LES refers to a broad set of techniques aiming at numerically simulating turbulent flows by representing accurately only those scales that are energetically significant. This approach is heuristically justified by Kolmogorov's estimate of the dimension of the attractor of the Navier--Stokes equation (whose existence is still a mystery at the present time in three space dimensions) that scales like 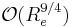${\mathc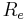al O}(R_e^{9/4})$ , where $R_e$ is the so-called Reynolds number and which in most industrial applications ranges in the interval $[10^6 , 10^9]$ . Considering the current pace of progress in computing power, this estimate undercuts the prospect of Direct Numerical Simulation (DNS) of large-Reynolds number flows to some date possibly far in the future.

Description

Fractional step methods

Fractional step methods are time stepping algorithms for approximating the incompressible Navier--Stokes equations. The objective of these algorithms is to uncouple viscous and incompressibility effects. This uncoupling greatly enhances the CPU performance of algorithms but may dramatically limit the accuracy. For instance, one of the most popular method, the so-called Chorin--Temam algorithm, is only first-order accurate in time (in adequate norms). The objective of this ongoing research project is to develop and mathematically justify new high-order, unconditionally stable, fractional step techniques.

Mathematical aspects of the LES

The LES techniques are essentially filtering and regularization techniques that aim at modeling the action of those small scales that cannot be represented numerically. LES is a quite young domain that is growing steadily. Surprisingly, this field has not yet attracted the attention of mathematicians, and a thorough mathematical analysis of LES has yet to be done. For instance, it is currently difficult to distinguish in this field an ad hoc numerical recipe from a theoretical profound result.

The research program I worked on between 1997 and 2006 consisted of defining (proposing) a mathematical framework for LES. I proposed the following definition:

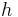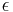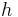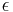A LES method is an algorithm with two parameters: the mesh size $h$ and the large eddy scale $\epsilon$ . The method must performs as follows when $h$ and $\epsilon$ go to zero:
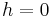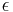When $h=0$ , and $\epsilon$ is fixed, one obtains a regularization technique for the three-dimensional Navier-Stokes equations. The regularization must be strong enough to ensure wellposedness.
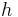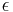There exists a distinguished limit on $h$ and $\epsilon$ so that the weak solution attained by this limit are suitable in the sense of Scheffer--Cafarelli--Khon--Nirenberg (roughly speaking, suitable solutions are those with no backscatter at very small scales, i.e. there is a scale below which energy goes down the scales. In some sense suitable solutions are entropic).

Results and prospect

Fractional step methods

I and J. Shen have recently revisited the so-called Chorin--Temam pressure-correction scheme and we have introduced two new class of methods that we called velocity-correction and consistent splitting. For both pressure-correction and velocity-correction methods we have introduced a variant that we called the rotational form. We proved new error estimates for the rotational variants. For instance we proved 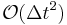${\mathcal O}(\Delta t^{2})$ convergence rate on the velocity in the 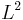$L^2$ -norm and 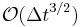${\mathcal O}(\Delta t^{3/2})$ convergence rate in the 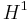$H^1$ -norm. These are the best error estimates available in the literature. This ongoing research is at the forefront of what is currently done in this field. At the present time there does not exists any fractional step technique with provable 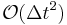${\mathcal O}(\Delta t^{2})$ error estimates in the 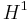$H^1$ -norm of the velocity (there are however many papers/methods claiming second order and higher on heuristic arguments, many of them being utterly wrong).

Mathematical aspects of the LES

I have proposed various Fourier-based methods that fit this definition. I think that this criterion is a good rationale for selecting good numerical methods. This definition is in the same spirit as defining a good numerical method for solving (scalar-valued) nonlinear conservation equations to be one that ensures that the weak solution obtained at the limit is the entropy solution.

This program lead us to wonder what the so-called Direct Numerical Simulation methods (DNS) really deliver. In this respect, I have proved two results that I think are very important:

The DNS solutions that are calculated in the periodic cube using finite elements, finite differences, or wavelets converge to suitable solutions in the sense of Scheffer--Cafarelli--Khon--Nirenberg. In other words, these methods have enough numerical dissipation to ensure that the energy dissipates correctly with no backscatter at very small scales. 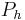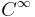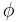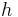The key mathematical argument behind this property is that there exists an interpolation operator $P_h$ so that for every $C^\infty$ function $\phi$ the commutator $[\phi,P_h]$ goes to zero fast enough as the mesh size $h$ goes to zero.
This result is true also with Dirichlet boundary conditions on the velocity.

Two above results prove that it is impossible to find a default if the energy cascade on solutions obtained with finite elements, finite differences, or wavelet. An interesting corollary of this result is that if one tries to numerically explore the possible enstrophy blow-up in the Navier-Stokes, it is recommended to use a spectral method.

This result also leads to the following question: Do the DNS solutions computed using spectral methods satisfy the entropy inequality of Scheffer--Cafarelli--Khon--Nirenberg? To the best of my knowledge, this problem is open. This question is really intriguing since most DNS computations aiming at studying turbulence are done using Fourier approximations. At the present time, there is no theorem ascertaining that the energy cascade for Fourier-based DNS solutions is correct. Proving (or disproving) that Scheffer--Cafarelli--Khon--Nirenberg entropy inequality holds for spectral DNS solutions is a mathematical problem that seems to me as hard (or slightly less) as proving uniqueness (which I recall is one of the "Clay" problem).

references

See publications

Links

Accueil > AERO >> AERO:Page_1