High order shock capturing schemes for LES of compressible flows

V. Daru, Y. Fraigneau and C. Tenaud

Object

Being an intermediary step between direct simulation and statistical description (RANS) for the calculation of turbulent flows, Large Eddy Simulation is a powerful method for the analysis of the dynamics of flows. In the compressible case, LES necessitates the use of numerical schemes capable to represent both the small structures of the flow with very low numerical dissipation, in order to minimize possible interactions with the subgrid model, and to capture discontinuities (shocks) with the robustness common to the Godunov type schemes. In [Daru et al. (2004)] we have developed a scheme, named OSMP7, which is designed to satisfy these two requirements. Preliminary numerical results on classical test cases have shown that the scheme could be a good candidate for LES simulations in the compressible case. We present here the results we obtained using OS7 / OSMP7 schemes for the computation of the turbulent supersonic channel flow.

Description

The OSMP7 scheme is an upwind, seventh order accurate in time and space (at least in the scalar case) explicit scheme. It is based on a coupled time-space Lax-Wendroff type approach, and a Strang splitting is used in the multidimensional case. For solving the Navier-Stokes equations, the scheme is formally only second order accurate due notably to the splitting. Nevertheless, the level of error of the scheme is very low, and it has been shown to give very accurate results for several test cases, using coarse meshes ([3],[4]). A monotonicity-preserving constraint is incorporated to the scheme, which is active only in the vicinity of steep gradients regions where it acts similarly to a TVD limiter. In such a way, no numerical oscillations are generated in calculating discontinuities (shock waves for instance). In smooth regions and in the vicinity of extrema of the solution, the monotonicity-preserving constraint is naturally satisfied implying that the limiting process is not activated, and the order of accuracy of the scheme is preserved. This is a very important difference with classical TVD schemes, for which accuracy degrades to first order near extrema with the effect of clipping extrema.

Results and Prospect

We here present a study that analyzes the behavior of the OS7 / OSMP7 schemes in the LES framework. The goal sought after is to estimate the potential interactions occurring between the high-order scheme and the subgrid-scale model. In this preliminary work, we have considered a supersonic turbulent infinite channel flow as relevant test-case to study the capability of the OS7 scheme to recover bounded turbulent flow behaviors.

Channel flow results

The Mach number is 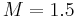, the Reynolds number based on the half height of the channel is 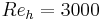. The channel is supposed periodic in the directions parallel to the walls The characteristics of the computational domain are given in Table 1. The mesh in the inhomogeneous direction is defined by a hyperbolic tangent function. Near the wall, the size of the first cell is about .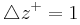

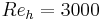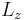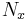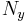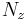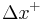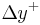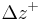
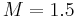
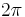
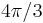
LES				2	41	61	119	33.5	15.	1.18

The initial condition is a Poiseuille flow with a uniform density. To force the transition to turbulence, a random perturbation with a finite amplitude is superimposed to the initial field. The periodicity condition in the flow direction necessitates the addition of an external force for ensuring mass flow rate conservation and equilibrating the losses due to viscous friction. The results are compared to the DNS results of [Coleman et al. (1995)] taken as reference results.

The LES computations use two kind of subgrid scale models. The first one is the compressible version of the mixed scale model derived in [Lenormand et al. (2000)]. This model smoothly damped the subgrid contributions in the regions where all turbulent structures are well resolved. The second model is the Mansour's formulation based however on a dynamical procedure to evaluate the model constant, following [Germano et al. (1991)]. A Reynolds analogy hypothesis (RAH), through a constant Prandtl number assumption, is employed to estimate the subgrid eddy conductivity. In a third LES modeling approach, a dynamical version of the former model has been used on both the dynamic scales and the thermal scales in order to overcome the constant turbulent Prandtl number assumption.

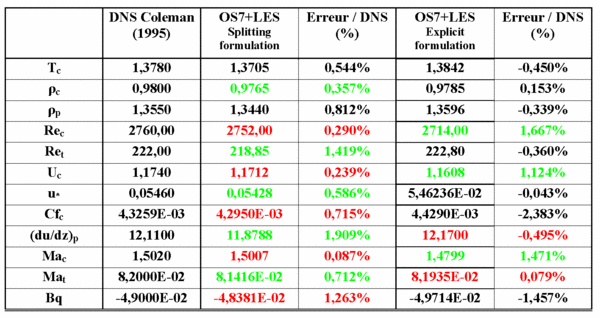
We show results about the way to implement the eddy viscosity model and hence, the coupling effect between the LES model and the OS7 scheme. For multi-dimensional configuration, the integration of equations with OS7 is carried out following a directional-splitting (Strang) procedure. Therefore, the temporal integration is split in successive steps, each one corresponds to an integration following one spatial direction. The basic OS7 scheme is moreover written by using a MacCormack procedure. Hence, each direction integration step contains two sub-steps due to the MacCormack procedure. To ensure the numerical consistency, the eddy viscosity may be updated at each sub-step (named splitting formulation). This procedure implies six updates per time-step. In the other way, we can consider the same value of the eddy viscosity over the whole time-step integration (named explicit formulation). Results are shown for these two approaches only by using the mixed-scale model. In table 2, we report the values of several quantities characterizing the flow. They are obtained from LES related to these two formulations and compared with DNS results of Coleman et al.

Table 2- LES of the supersonic turbulent channel flow using the OS7 scheme: characteristic values for two mixed-scale model implementations (splitting and explicit formulations) compared to the DNS reference values; the red values are the most accurate and the green ones the worst.

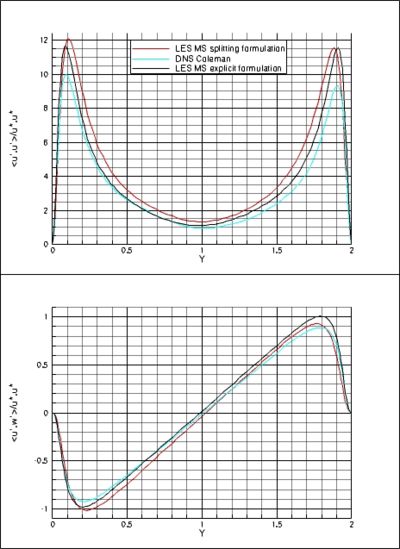
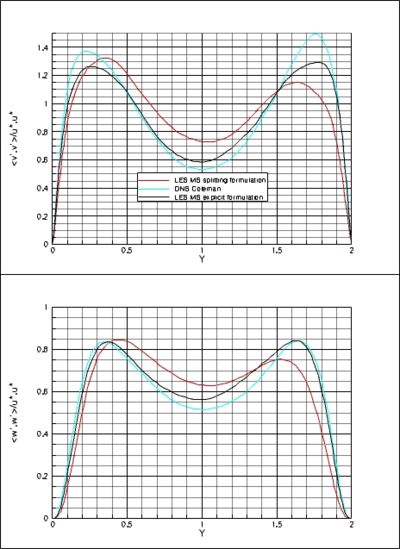
The LES values are in very good agreement with the DNS references. Globally, the discrepancies are close to 1% and less than 3% for the worst. Nevertheless, the profiles of mean quantities and the Reynolds stress components (i.e. the turbulent shear stress) (Figure 1) show a more pronounced non-symmetric behaviour by using the splitting formulation. This non-symmetric behavior might be overcome by using longer time integrations but without a real benefit on the result quality. In our simulations, the time scale range used to calculate the statistical quantities is sufficiently large (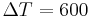) to limit the non-symmetric effect. This phenomenon is a direct consequence of the splitting formulation that generates an artificial numerical anisotropic effect and enforces the non-symmetric behavior. On the opposite, the explicit formulation gives much better results by significantly reducing the non-symmetric behavior.

Figure 1: LES of the supersonic turbulent channel flow using the OS7 scheme: Influence of the the subgrid-scale model implementation on the Reynolds stress components.

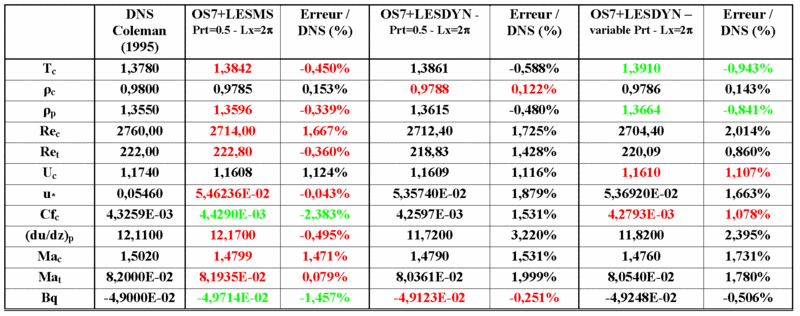
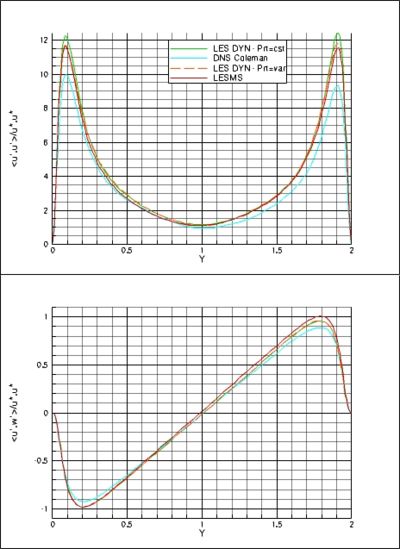
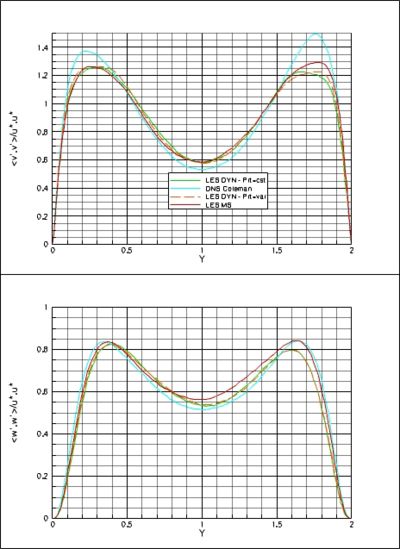
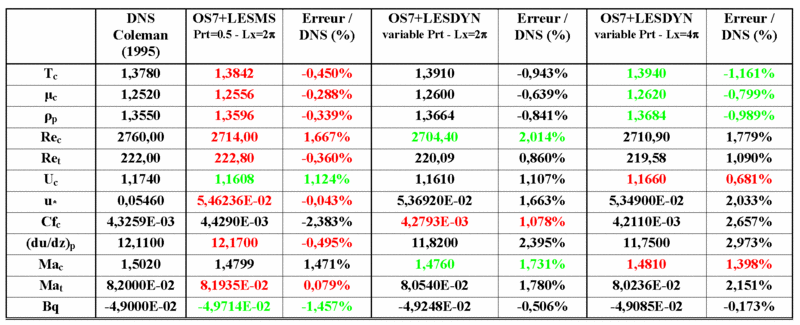
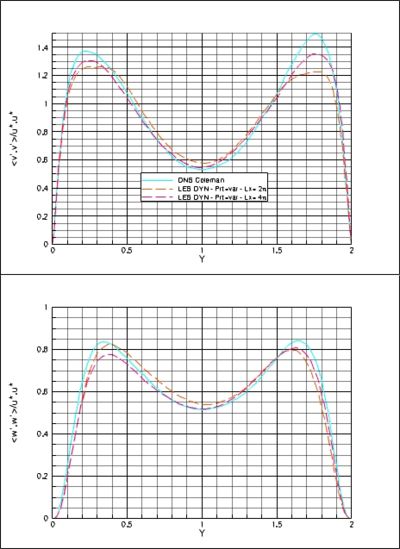
Then, we have compared LES results issued from mixed-scale modeling and the Mansour's formulation coupled with a dynamical procedure either with a constant turbulent Prandtl number (equal to 0.5) or with a variable turbulent Prandtl number evaluated through a dynamical procedure. The results concerning some relevant characteristic quantities of the flow are reported table 3.

Table 3- LES of the supersonic turbulent channel flow using the OS7 scheme: characteristic values obtained by using several subgrid scale model approaches are compared to the DNS reference values; the red values are the most accurate and the green ones the worst.

The discrepancies are of the same order whatever the model procedure used while the dynamical procedure recovers a slightly better wall heat flux. This is confirmed on the profiles where no significant differences can be seen (Figure 2). The peak locations in the profiles agree very well with the reference. On the rms-value profiles, a slightly better results are achieved with the Mixed-Scale model while the dynamical procedure gives slightly better accurate profiles on the turbulent shear-stress and normal heat-flux. Considering a variable turbulent Prandtl number in the dynamical procedure does not significantly enhance the LES results.

Figure 2: LES of the supersonic turbulent channel flow using the OS7 scheme: Influence of the subgrid-scale model apprach on the Reynolds stress components.

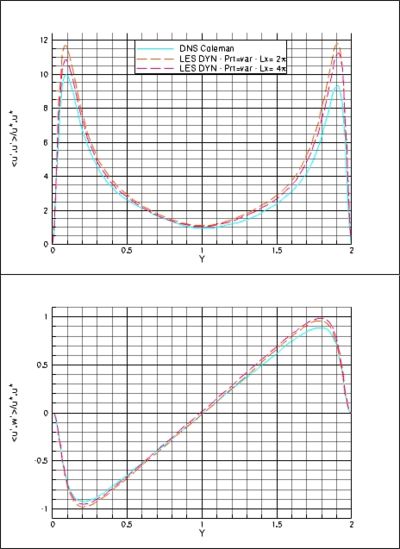
Finally, we studied the influence of the length of the computational domain. No significant discrepancies can be noticed both on the characteristic values (Table 4) and on the mean and fluctuating profiles (Figure 3).

Table 4- LES of the supersonic turbulent channel flow using the OS7 scheme: characteristic values obtained by using two different lengths of the computational domain are compared to the DNS reference values; the red values are the most accurate and the green ones the worst.

Figure 3: LES of the supersonic turbulent channel flow using the OS7 scheme: Influence of the computational domain length on the Reynolds stress components.

Conclusion and prospects

The capability of the OS7 scheme in the LES framework have been reviewed on the supersonic turbulent channel flow test-case. Several subgrid scale models have been used: the mixed-scale model and the dynamical procedure on the Mansour model. The influence of the dynamical procedure have also been reviewed on the thermal scales considering variable subgrid Prandtl number. Results show that the sensitivity of the results to the different models used is weak. This is not surprising because all the models used are based on the same approach through the Mansour's model. This test-case seems to be weakly sensitive to the subgrid thermal scales. Nevertheless, the discrepancies observed between each model results are of the same order compared to the DNS reference. We observed non-symmetric profile behavior either in LES or DNS results that are of the same order of magnitude in both cases.

The next step of this research will be to carry out LES simulations of compressible turbulent flows with shock-waves, using the OSMP7 scheme. As far as shock-waves are concerned, we have to evaluate the influence of the limiting process based on the 'Monotonicity-Preserving constraints on the turbulent characteristics of the flow. This study is actually in progress.

Refrences

1. Coleman G. N., Kim J. and Moser R. D. (1995), A numerical study of turbulent supersonic isothermal-wall channel flow, J. Fluid Mech., 305: 159-183 .
2. Daru V., Tenaud C. (2004), High order one-step monotonicity-preserving schemes for unsteady compressible flow calculations, J. Comput. Phys., 193: 563-594.
3. Daru V., Tenaud C. (2004), Numerical simulation of the shock wave/boundary layer interaction in a shock tube by using a high resolution monotonicity-preserving scheme. Proceedings of the International Conference on Computational Fluid Dynamics, Toronto, Canada, 12-16 July 2004.
4. Daru V., Fraigneau Y., Tenaud C. (2005), Comportement d'un schéma à capture de choc de haute précision en Simulation des Grandes Echelles. Actes du Congrès Français de Mécanique, Troyes, 29 août-2 Septembre 2005.
5. Doris L., Tenaud C. and Ta Phuoc L. (2000), LES of spatially developing 3D compressible mixing layer, C.R. Acad. Sci. Paris, Série II b, 328: 567-573.
6. Edwards J., Liou M. S. (1998), Low-diffusion flux-splitting methods for flows at all speeds, AIAA J., 36: 1610-1617.
7. M. Germano, U. Piomelli, P. Moin and W. H. Cabot (1991), A dynamic subgrid-scale eddy viscosity model, Physics of Fluids A 3: 1760-1765.
8. Lenormand E., Sagaut P., Ta Phuoc L. and Comte P. (2000), Subgrid-Scale Models for Large-Eddy Simulations of Compressible Wall Bounded Flows, AIAA J., vol. 38: 1340-1350.

Links

AERO